Question

The circle $x^{2}+y^{2}+2ax+c=0$ and $x^{2}+y^{2}+2by+c=0$ touch if,
A) $\dfrac{1}{a^{2}} +\dfrac{1}{b^{2}} =\dfrac{1}{c}$
B) $\dfrac{1}{a^{2}} +\dfrac{1}{b^{2}} =\dfrac{1}{c^{2}}$
C) $\dfrac{1}{a} +\dfrac{1}{b} +\dfrac{1}{c} =0$
D) None of these.

Answer 1

Hint: In this question it is given that two circle $x^{2}+y^{2}+2ax+c=0$ and $x^{2}+y^{2}+2by+c=0$ touches each other, we have to find the relation between a,b and c. So first of all we draw the diagram.

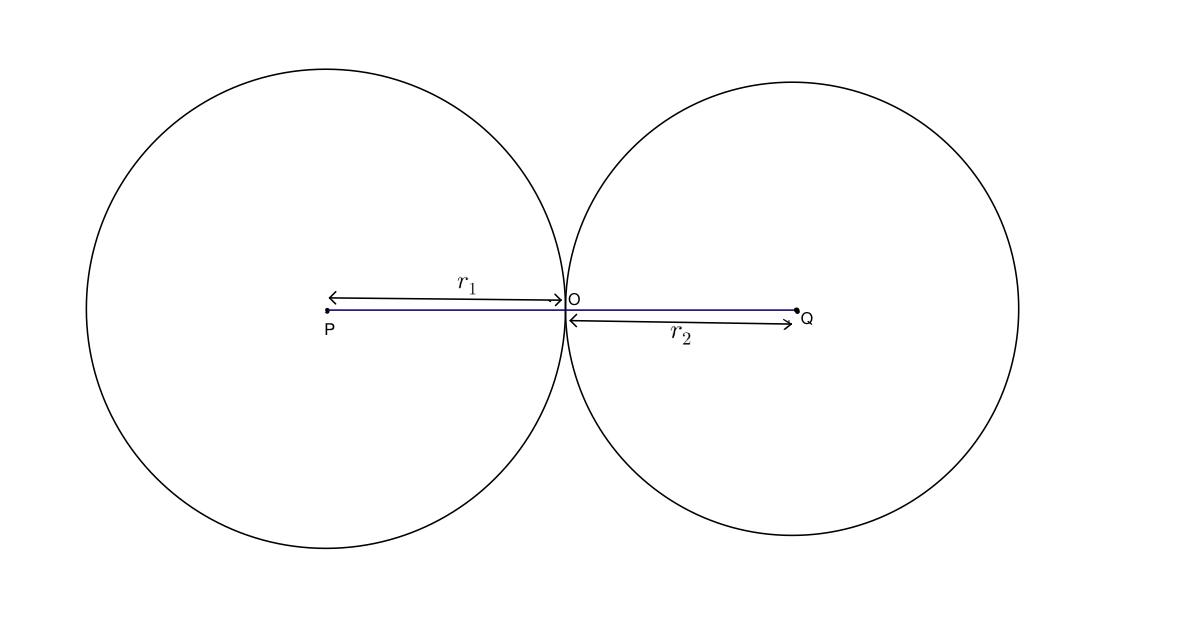
So for finding the solution we need to find the coordinates of the centres of the circles and their radius,and from the diagram we can write the distance between the centres is equal to the summation of their radius,i.e, $r_{1}+r_{2}$=PQ.

Complete step-by-step solution:
Consider the circle $x^{2}+y^{2}+2ax+c=0$ whose centre is P and radius is $r_{1}$ and and another circle $x^{2}+y^{2}+2by+c=0$ with centre Q and radius $r_{2}$.
Now as we know that if any equation of circle is in the form of $x^{2}+y^{2}+2gx+2fy+c=0$.......(1)
Then the coordinate of the centre is (-g,-f) and radius is $\sqrt{g^{2}+f^{2}-c}$.
Now by equation (1) we can say that the centre of circle $x^{2}+y^{2}+2ax+c=0$ is P(-a,0) and radius is $r_{1}=\sqrt{\left( -a\right)^{2} +0^{2}-c} =\sqrt{a^{2}-c}$.
Similarly, the coordinate of centre and the radius of the circle $x^{2}+y^{2}+2by+c=0$ is Q(0,-b) and $r_{2}=\sqrt{b^{2}-c}$.
Now To find the distance PQ, we have to know the distance formula i.e, the distance between the points (a,b) to (c,d) is $\mathbf{d} =\sqrt{\left( a-c\right)^{2} +\left( b-d\right)^{2} }$ ............equation(2)
Now by equation (2) we can write,
PQ=$\sqrt{\left( -a-0\right)^{2} +\left( 0-\left( -b\right) \right)^{2} }$
=$\sqrt{a^{2}+b^{2}}$.
Since, as we know that the distance between the centres is equal to the summation of their radius, so we can write,
$r_{1}+r_{2}$=PQ
$\Rightarrow \sqrt{a^{2}-c} +\sqrt{b^{2}-c} =\sqrt{a^{2}+b^{2}}$
By squaring both side, we get,
$\left( \sqrt{a^{2}-c} +\sqrt{b^{2}-c} \right)^{2} =\left( \sqrt{a^{2}+b^{2}} \right)^{2}$
$\Rightarrow \left( \sqrt{a^{2}-c} \right)^{2} +2\sqrt{a^{2}-c} \sqrt{b^{2}-c} +\left( \sqrt{b^{2}-c} \right)^{2} =a^{2}+b^{2}$
$\Rightarrow a^{2}-c+2\sqrt{a^{2}-c} \sqrt{b^{2}-c} +b^{2}-c=a^{2}+b^{2}$
$\Rightarrow 2\sqrt{a^{2}-c} \sqrt{b^{2}-c} -2c=0$ [canceling $a^{2}$ and $b^{2}$]
$\Rightarrow \sqrt{a^{2}-c} \sqrt{b^{2}-c} =c$
Again squaring both side of the above equation,
$\left( \sqrt{a^{2}-c} \sqrt{b^{2}-c} \right)^{2} =c^{2}$
$\Rightarrow \left( a^{2}-c\right) \left( b^{2}-c\right) =c^{2}$
$\Rightarrow a^{2}b^{2}-a^{2}c-b^{2}c+c^{2}=c^{2}$
$\Rightarrow a^{2}b^{2}-a^{2}c-b^{2}c=0$
$\Rightarrow a^{2}c+b^{2}c=a^{2}b^{2}$
Now dividing both side of the above equation by $a^{2}b^{2}c$ we get,
$\dfrac{1}{b^{2}} +\dfrac{1}{a^{2}} =\dfrac{1}{c}$
$\Rightarrow \dfrac{1}{a^{2}} +\dfrac{1}{b^{2}} =\dfrac{1}{c}$
Which is our required condition.
Thus the correct option is option A.

Note: To solve this type of question you need to know that whenever two circles touch each other, then the distance between their centre is equal to the summation of their radius.