Solveeit Logo
Login

Question

Question: The circle with centre (2, 3) and intersecting \[{{\rm{x}}^2}{\rm{ + }}{{\rm{y}}^2}{\rm{ - 4x + 2y -...

The circle with centre (2, 3) and intersecting x2+y2−4x+2y−7=0{{\rm{x}}^2}{\rm{ + }}{{\rm{y}}^2}{\rm{ - 4x + 2y - 7 = 0}} orthogonally has the radius.
A) 1
B) 2
C) 3
D) 4

Explanation

Solution

Here we have to find out the radius of the circle. Firstly we will find out the radius and the centre of the intersecting circle. Then we will apply Pythagoras theorem to find out the radius of the circle as we will know the centre to centre distance and also the radius of the intersecting circle. So by that we will be able to find out the radius of the circle.

Complete step by step solution:
Equation of the intersecting circle is x2+y2−4x+2y−7=0{{\rm{x}}^2}{\rm{ + }}{{\rm{y}}^2}{\rm{ - 4x + 2y - 7 = 0}}………. (1)
We know that circle with centre (p, q) and radius r have a equation of (x−p)2+(y−q)2=r2{{\rm{(x - p)}}^2}{\rm{ + (y - q}}{{\rm{)}}^2}{\rm{ = }}{{\rm{r}}^2}………. (2)
We can write the equation (1) as x2+4−4x+y2+1+2y−12=0{{\rm{x}}^2}{\rm{ + 4 - 4x + }}{{\rm{y}}^2}{\rm{ + 1 + 2y}} - 12 = 0
Above equation can be written as (x−2)2+(y+1)2=(12)2{{\rm{(x - 2)}}^2}{\rm{ + (y + 1}}{{\rm{)}}^2}{\rm{ = (}}\sqrt {12} {)^2} if we will compare this equation with the equation (2) we get the centre of the circle as (2, -1) and radius as 12\sqrt {12}

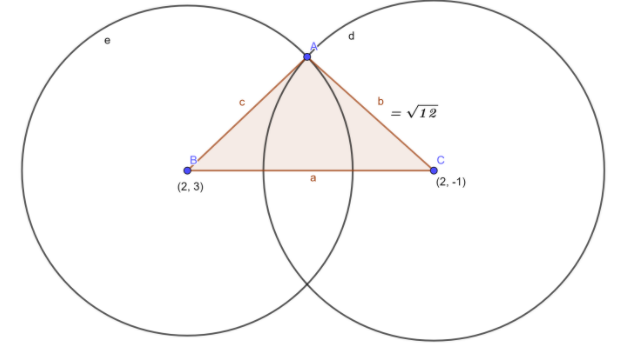
Now we have to find out the distance between the centers i.e. BC.
BC=(2−2)2+(−1−3)2=0+(−4)2=16=4{\rm{BC = }}\sqrt {{{(2 - 2)}^2} + {{( - 1 - 3)}^2}} {\rm{ = }}\sqrt {0 + {{( - 4)}^2}} {\rm{ = }}\sqrt {16} {\rm{ = 4}}
Now we have to apply Pythagoras theorem in the right triangle ABC to get the value of the radius of the other circle.
Therefore, BC2=AB2+AC2{\rm{B}}{{\rm{C}}^2}{\rm{ = A}}{{\rm{B}}^2}{\rm{ + A}}{{\rm{C}}^2} where,BC=4{\rm{BC = 4}},AC=12{\rm{AC = }}\sqrt {12} and we have to find the value of AB, we get
⇒16=AB2+12\Rightarrow 16 = {\rm{A}}{{\rm{B}}^2}{\rm{ + }}12
⇒AB2=4\Rightarrow {\rm{A}}{{\rm{B}}^2}{\rm{ = 4}}
⇒AB=4=2\Rightarrow {\rm{AB = }}\sqrt {\rm{4}} {\rm{ = 2}}

Hence, the radius of the circle is equal to 2 units.
So, option B is correct.

Note:
Two circles are said to be orthogonal if the tangents to the both circles at the point of intersection makes 900{90^0} angle with each other i.e. perpendicular to each other then circles are aid that they are orthogonal to each other. Any symmetrical shape can intersect any other symmetric shape orthogonally. We should know the basic equation of the circle having centre (p, q) and radius r have a equation of (x−p)2+(y−q)2=r2{{\rm{(x - p)}}^2}{\rm{ + (y - q}}{{\rm{)}}^2}{\rm{ = }}{{\rm{r}}^2}.
Pythagoras theorem stated that In a right angled triangle the square of the long side is equal to the sum of the squares of the other two sides.