Question

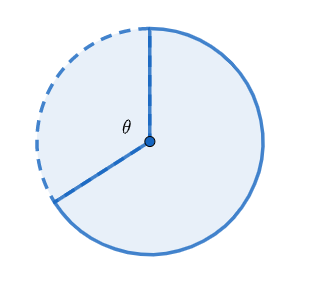
The circle shown below has a diameter of 18 centimeters (cm). If the dotted arc is 33 cm long, what is the measure of angle $\theta$ in radians?

A. $\dfrac{3}{11}$
B. $\dfrac{6}{11}$
C. $\dfrac{11}{6}$
D. $\dfrac{11}{3}$

Answer 1

To find the measure of the angle $\theta$ , we will use the formula for the length of an arc of a sector which is given as $l=\dfrac{\theta }{2\pi }\times \pi D$ , where $\theta$ is the angle of the sector, $2\pi$ is the angle of the circle in radian and $\pi D$ is the circumference of the circle. On substituting the values and simplifying, we will get the correct option.

Complete step-by-step solution:
We need to find the measure of the angle $\theta$ . We are given that arc length =33 cm
Diameter of the circle =18 cm
We know that, the length of an arc of a sector is given as
$l=\dfrac{\theta }{2\pi }\times 2\pi r...\left( i \right)$ , where $\theta$ is the angle of the sector, $2\pi$ is the angle of the circle in radian and $2\pi r$ is the circumference of the circle.
We know that the diameter of a circle is twice its radius.
$D=2r$
Hence, we can write the formula (i) as
$l=\dfrac{\theta }{2\pi }\times \pi D$
Let us simplify this formula by cancelling $\pi$ from numerator and denominator.
$l=\dfrac{\theta }{2}\times D$
We need to find $\theta$ . So let us collect all the other terms to one side. We will get
$\theta =\dfrac{2l}{D}$
Now, let us substitute the values.
$\theta =\dfrac{2\times 33}{18}$
On solving, we will get
$\theta =\dfrac{33}{9}=\dfrac{11}{3}\text{ rad}$
Hence, the correct option is D.

Note: We can also write the length of the arc as $l=\dfrac{\theta }{{{360}^{{}^\circ }}}\times \pi D$ , when the angle is in degrees. Students must always check the units specified in the question and solve them accordingly.