Question

The circle 'S' touches the sides AB and AD of the rectangle ABCD and cuts the side DC at single point F and the side BC at a single point E. If |AB| = 32,|AD| = 40 and|BE| =1

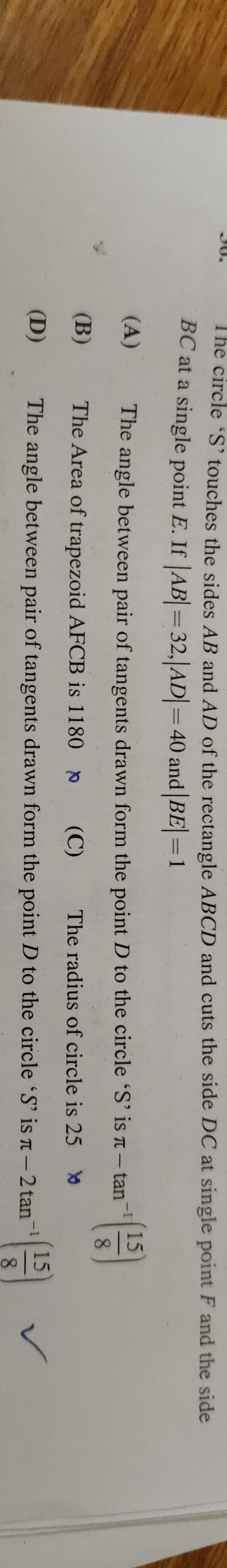
• A. The angle between pair of tangents drawn form the point D to the circle 'S' is $\pi - tan^{-1}(\frac{15}{8})$
• B. The Area of trapezoid AFCB is 1180
• C. The radius of circle is 25
• D. The angle between pair of tangents drawn form the point D to the circle 'S' is $\pi – 2 tan^{-1}(\frac{15}{8})$

Answer 1

Answer: (A), (B), (C)

A, B, C

Answer 2

1. Understanding the Geometry and Setup: Let the rectangle ABCD be placed in the Cartesian coordinate system with vertex A at the origin (0,0). Given |AB| = 32 and |AD| = 40. The coordinates of the vertices are: A = (0,0) B = (32,0) C = (32,40) D = (0,40)

   The sides of the rectangle lie on the lines: AB: y = 0 AD: x = 0 BC: x = 32 DC: y = 40

   The circle 'S' touches sides AB and AD. This means the circle is tangent to the x-axis (y=0) and the y-axis (x=0). If the radius of the circle is $r$, its center must be at $(r, r)$ and its equation is $(x-r)^2 + (y-r)^2 = r^2$.

   The circle cuts the side DC (line y=40) at a single point F. The circle cuts the side BC (line x=32) at a single point E.

2. Evaluating Option (C) - Radius: Let's test Option (C): The radius of the circle is 25. If $r=25$, the center of the circle is Ctr = (25, 25). The equation of the circle is $(x-25)^2 + (y-25)^2 = 25^2$.

   • Intersection with DC (y=40): Substitute y=40: $(x-25)^2 + (40-25)^2 = 25^2 \implies (x-25)^2 + 15^2 = 25^2 \implies (x-25)^2 = 400 \implies x-25 = \pm 20$. The x-coordinates are $x_1 = 45$ and $x_2 = 5$. Since DC extends from x=0 to x=32, the point F=(5,40) is on DC. The other point is outside. This matches the description.

   • Intersection with BC (x=32): Substitute x=32: $(32-25)^2 + (y-25)^2 = 25^2 \implies 7^2 + (y-25)^2 = 25^2 \implies (y-25)^2 = 576 \implies y-25 = \pm 24$. The y-coordinates are $y_1 = 49$ and $y_2 = 1$. Since BC extends from y=0 to y=40, the point E=(32,1) is on BC. The other point is outside. This matches the description.

   • Given condition |BE| = 1: B=(32,0) and E=(32,1). The distance |BE| = $\sqrt{(32-32)^2 + (1-0)^2} = 1$. This condition is satisfied. Since all conditions are met with $r=25$, Option (C) is correct.

3. Evaluating Option (A) and (D) - Angle of Tangents from D: The point D is (0,40). The center of the circle is Ctr = (25,25), and the radius is $r=25$. The distance CD = $\sqrt{(25-0)^2 + (25-40)^2} = \sqrt{25^2 + (-15)^2} = \sqrt{625 + 225} = \sqrt{850}$. Let $\alpha$ be the angle between CD and the radius to a point of tangency. In the right triangle formed by D, Ctr, and a tangent point, $\sin(\alpha) = \frac{r}{CD} = \frac{25}{\sqrt{850}} = \frac{5}{\sqrt{34}}$. Then $\cos(\alpha) = \sqrt{1 - (\frac{5}{\sqrt{34}})^2} = \sqrt{1 - \frac{25}{34}} = \sqrt{\frac{9}{34}} = \frac{3}{\sqrt{34}}$. $\tan(\alpha) = \frac{5/{\sqrt{34}}}{3/{\sqrt{34}}} = \frac{5}{3}$. The angle between the two tangents drawn from D is $\phi = 2\alpha$. Using the double angle formula for tangent: $\tan(2\alpha) = \frac{2\tan(\alpha)}{1 - \tan^2(\alpha)} = \frac{2(5/3)}{1 - (5/3)^2} = \frac{10/3}{1 - 25/9} = \frac{10/3}{-16/9} = -\frac{15}{8}$. If $\tan(2\alpha) = -15/8$, then $2\alpha = \arctan(-15/8)$. Since $2\alpha$ must be an angle between 0 and $\pi$ for tangents from an external point, and $\tan(2\alpha)$ is negative, $2\alpha$ is in the second quadrant. Let $\beta = \tan^{-1}(15/8)$ (an acute angle). Then $\tan(\pi - \beta) = -\tan(\beta) = -15/8$. So, $2\alpha = \pi - \tan^{-1}(15/8)$. Option (A) is correct. Option (D) suggests $2\alpha = \pi - 2\tan^{-1}(15/8)$. This would mean $\tan(2\alpha) = \tan(\pi - 2\beta) = -\tan(2\beta)$. $\tan(2\beta) = \frac{2(15/8)}{1-(15/8)^2} = \frac{15/4}{1-225/64} = \frac{15/4}{-161/64} = -\frac{240}{161}$. So, $-\tan(2\beta) = \frac{240}{161} \neq -15/8$. Option (D) is incorrect.

4. Evaluating Option (B) - Area of Trapezoid AFCB: The coordinates are A=(0,0), F=(5,40), C=(32,40), B=(32,0). The parallel sides are AB (on y=0) and FC (on y=40). Length of AB = 32. Length of FC = $32 - 5 = 27$. The height of the trapezoid is the distance between y=0 and y=40, which is $h=40$. Area $= \frac{1}{2} (AB + FC) \times h = \frac{1}{2} (32 + 27) \times 40 = \frac{1}{2} (59) \times 40 = 59 \times 20 = 1180$. Option (B) is correct.