Question

The circle ${C_1}:{x^2} + {y^2} = 3$ , with centre at O, intersect the parabola ${x^2} = 2y$ at the point P in the first quadrant. Let the tangent to the circle ${C_1}$ at P touches other two circles ${C_2}$and ${C_3}$at ${R_2}$ and ${R_3}$, respectively. Suppose ${C_2}$and ${C_3}$ have equal radii $2\sqrt 3$ and centres ${Q_2}$ and ${Q_3}$ , respectively. If ${Q_2}$ and ${Q_3}$lie on the y-axis, then which of the following is correct?
(A) ${Q_2}{Q_3} = 12$
(B) ${R_2}{R_3} = 4\sqrt 6$
(C) Area of the triangle $O{R_2}{R_3}$ is $6\sqrt 2$
(D) Area of the triangle $P{Q_2}{Q_3}$ is $4\sqrt 2$

Answer 1

Use the given information in the question to draw a diagram on the coordinate plane. Represent all the information in the diagram properly. Now solve for each of the options one by one. For (A), assume points ${Q_2}$ and ${Q_3}$as $\left( {0,{q_2}} \right){\text{ and }}\left( {0,{q_3}} \right)$ since they lie on the y-axis and use the distance formula $\left| {\dfrac{{a{x_1} + b{y_1} + c}}{{\sqrt {{a^2} + {b^2}} }}} \right|$. For (B) use the formula for transverse common tangent in both circles ${Q_2}{\text{ and }}{Q_3}$ .

Complete step-by-step answer:

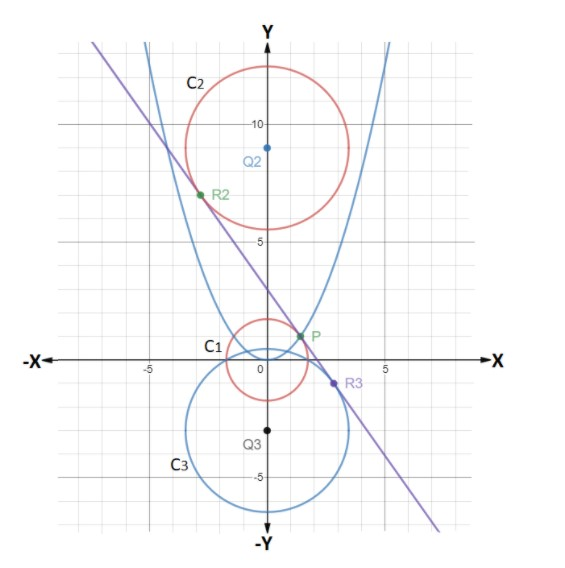
Let’s first start with analyzing the question using a diagram. Firstly draw a circle ${C_1}:{x^2} + {y^2} = 3$ , which is centred at $O\left( {0,0} \right)$ and has a radius $\sqrt 3 {\text{ units}}$. And a parabola ${x^2} = 2y$, which is an upward open parabola with vertex at $O\left( {0,0} \right)$ and axis as the y-axis. In the first quadrant, these two curves intersect at point P. From point P a tangent to a circle ${C_1}$is drawn.
Now, this tangent line also touches the circle ${C_2}{\text{ and }}{C_3}$, which are centred at ${Q_2}{\text{ and }}{Q_3}$ on y-axis. The point of contact of line and two circles is at ${R_2}{\text{ and }}{R_3}$. So the tangent of the circle ${C_1}$ from point P is also a tangent to circle ${C_2}{\text{ and }}{C_3}$. The radius of the circle ${C_2}{\text{ and }}{C_3}$is $2\sqrt 3$
Let’s first find the coordinates of point P. Since this point lies in the first quadrant, both the coordinates will be positive for P.
Assuming $P\left( {x,y} \right)$ lies on both ${x^2} = 2y$ and ${x^2} + {y^2} = 3$. Substituting the value ${x^2} = 2y$ in the equation of the circle:
$\Rightarrow 2y + {y^2} = 3 \Rightarrow {y^2} + 3y - y - 3 = 0 \Rightarrow \left( {y - 1} \right)\left( {y + 3} \right) = 0$
Therefore, we get: $y = 1{\text{ and }}y = - 3$ . But for the required point, we need a positive value of coordinates.
Hence, we can conclude:$y = 1$ . Putting this in the equation of the circle to find the x-coordinate:
$\Rightarrow {x^2} + {1^2} = 3 \Rightarrow x = \sqrt {3 - 1} = \sqrt 2$
So, the coordinates of point P is $\left( {\sqrt 2 ,1} \right)$
Now, we need to find the equation of tangent from the point $\left( {\sqrt 2 ,1} \right)$ for the circle ${x^2} + {y^2} = 3$
As we know that the equation of the tangent at the point $\left( {{x_1},{y_1}} \right)$ for a circle with equation ${x^2} + {y^2} = {a^2}$ can be written as: $x{x_1} + y{y_1} = {a^2}$
Using the above relation, we can say that the equation of tangent from the point $\left( {\sqrt 2 ,1} \right)$ for the circle ${x^2} + {y^2} = 3$ will be: $x \times \sqrt 2 + y \times 1 = 3 \Rightarrow \sqrt 2 x + y = 3$
So now we need to find the coordinates for the point ${Q_2}{\text{ and }}{Q_3}$. We know that the above line is the tangent to the circles ${C_2}$and ${C_3}$, hence the radius of these circles ${R_2}{Q_2}$ and ${R_3}{Q_3}$ will be perpendicular to the line.
Since we know that the shortest distance between a point $\left( {{x_1},{y_1}} \right)$ and the line $ax + by + c = 0$ can be given by $\left| {\dfrac{{a{x_1} + b{y_1} + c}}{{\sqrt {{a^2} + {b^2}} }}} \right|$
If we use this relation to find the distance between the line $\sqrt 2 x + y = 3$ and point ${Q_2}$, we can equate the distance with the given measure of radius, i.e. $2\sqrt 3$
Assuming that the coordinates of the point ${Q_2}{\text{ and }}{Q_3}$ be $\left( {0,{q_2}} \right){\text{ and }}\left( {0,{q_3}} \right)$ , as they lie on the y-axis
$\Rightarrow \left| {\dfrac{{\sqrt 2 \times 0 + 1 \times {q_2} - 3}}{{\sqrt {{{\left( {\sqrt 2 } \right)}^2} + {1^2}} }}} \right| = 2\sqrt 3 \Rightarrow \left| {\dfrac{{{q_2} - 3}}{{\sqrt 3 }}} \right| = 2\sqrt 3 \Rightarrow {q_2} - 3 = 2\sqrt 3 \times \sqrt 3 \Rightarrow {q_2} = 6 + 3 = 9$
Similarly, for circle ${C_3}$but remember that ${q_3}$ lies on the negative side of the y-axis and thus while resolving the absolute value function it will bring a negative sign on another side of the equation :
$\Rightarrow \left| {\dfrac{{\sqrt 2 \times 0 + 1 \times {q_3} - 3}}{{\sqrt {{{\left( {\sqrt 2 } \right)}^2} + {1^2}} }}} \right| = 2\sqrt 3 \Rightarrow \left| {\dfrac{{{q_3} - 3}}{{\sqrt 3 }}} \right| = 2\sqrt 3 \Rightarrow {q_3} - 3 = - 2\sqrt 3 \times \sqrt 3 \Rightarrow {q_3} = - 6 + 3 = - 3$
Therefore, we got the coordinates of a point ${Q_2}{\text{ and }}{Q_3}$ as $\left( {0,9} \right){\text{ and }}\left( {0, - 3} \right)$
Hence, the distance ${Q_2}{Q_3}$ will be ${Q_2}{Q_3} = \sqrt {{{\left( {0 - 0} \right)}^2} + {{\left( {9 - \left( { - 3} \right)} \right)}^2}} = \sqrt {{{\left( {12} \right)}^2}} = 12$
Let's check for Option B.
Now, we need to find the length${R_2}{R_3}$. According to our diagram, these points lie on the line $\sqrt 2 x + y = 3$ and on the respective circles.
As we know that the length of the transverse common tangent can be written as $\sqrt {{{\left( {{Q_2}{Q_3}} \right)}^2} - {{\left( {{r_2} + {r_3}} \right)}^2}}$
$\Rightarrow {R_2}{R_3} = \sqrt {{{12}^2} - {{\left( {2\sqrt 3 + 2\sqrt 3 } \right)}^2}} = \sqrt {144 - 48} = \sqrt {96} = 4\sqrt 6$
Let's check for Option C
Now we have to find the area of the triangle $O{R_2}{R_3}$. In $\Delta O{R_2}{R_3}$ we have ${R_2}{R_3}$ as its base and OP as its altitude, which is also the radius of the circle ${C_1}$ .
As we know, the area of a triangle is half times its base times its altitude.
$\Rightarrow$ Area of $\Delta O{R_2}{R_3} = \dfrac{1}{2} \times base \times altitude = \dfrac{1}{2} \times {R_1}{R_2} \times OP$
Now, substituting the values of ${R_2}{R_3}$ and OP from the above results, we get:
$\Rightarrow$ Area of $\Delta O{R_2}{R_3} = \dfrac{1}{2} \times {R_2}{R_3} \times OP = \dfrac{1}{2} \times 4\sqrt 6 \times \sqrt 3 = 2\sqrt {18} = 6\sqrt 2 sq.units$
Let's check for Option D
Now, let’s find the area of $\Delta P{Q_2}{Q_3}$ . In $\Delta P{Q_2}{Q_3}$ , we have ${Q_2}{Q_3}$ as its base and the perpendicular from point P to the y-axis as its altitude.
So, as we know the coordinates of point P as $\left( {\sqrt 2 ,1} \right)$, i.e. it distance from y-axis is $\sqrt 2 units$ and distance from x-axis is $1unit$ . Hence, the perpendicular distance from ${Q_2}{Q_3}$ to point P , i.e. altitude of $\Delta P{Q_2}{Q_3}$ will be $\sqrt 2 units$.
$\Rightarrow$ Area of $\Delta P{Q_2}{Q_3} = \dfrac{1}{2} \times base \times altitude = \dfrac{1}{2} \times {Q_2}{Q_3} \times altitude$
After substituting the values, we get:
$\Rightarrow$ Area of $\Delta P{Q_2}{Q_3} = \dfrac{1}{2} \times base \times altitude = \dfrac{1}{2} \times 12 \times \sqrt 2 = 6\sqrt 2 sq.units$

So, the correct answer is “Option A ,B and C”.

Note: In coordinate geometry, the diagram is a crucial part of the solution. It is important to understand the given information in the question and represent it on the coordinate plane. The distance between two points can be determined using the square root of the sum of squares of the difference of the coordinates. That’s what we used to find the distance ${Q_2}{Q_3}$from the point ${Q_2}$ and ${Q_3}$.
And the length of the transverse common tangent can be written as the square root of the difference of the square of the distance between centres of the circle and the square of the sum of the radius of both circles. This was used to find the length of the transverse common tangent ${R_2}{R_3}$.