Question

The chord of contact of tangents drawn from any point on the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ to the circle ${{x}^{2}}+{{y}^{2}}={{b}^{2}}$ touches the circle ${{x}^{2}}+{{y}^{2}}={{c}^{2}}$ . Show that a, b and c are in GP.

Answer 1

Now first let us consider point $\left( {{x}_{1}},{{y}_{1}} \right)$ on the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ . Now we will write the equation of tangent from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the circle ${{x}^{2}}+{{y}^{2}}={{b}^{2}}$ Now equation of tangent drawn from point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the circle ${{x}_{1}}^{2}+{{y}_{1}}^{2}={{b}^{2}}$ is given by $x{{x}_{1}}+y{{y}_{1}}={{b}^{2}}$ . Now we know that this line is tangent to the circle ${{x}^{2}}+{{y}^{2}}={{c}^{2}}$ hence we can say that the perpendicular drawn from the center of the circle to this line is equal to radius. Hence using this we will find the relation in a, b and c.

Complete step by step answer:

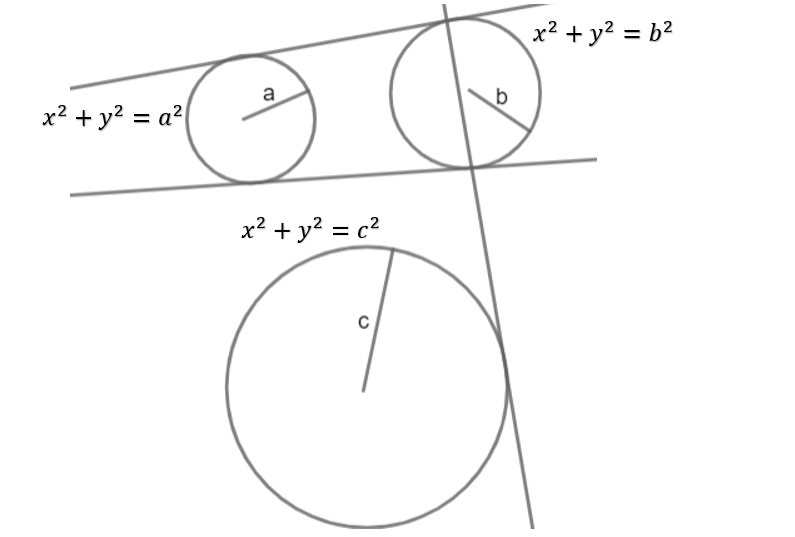
Now first consider the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$
Let us say we have a point $\left( {{x}_{1}},{{y}_{1}} \right)$on this circle.
Hence we get, ${{x}_{1}}^{2}+{{y}_{1}}^{2}={{a}^{2}}$ .
Now equation of tangent drawn from point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the circle ${{x}_{1}}^{2}+{{y}_{1}}^{2}={{b}^{2}}$ is given by $x{{x}_{1}}+y{{y}_{1}}={{b}^{2}}$ .
Now we are given that this line touches the circle ${{x}_{1}}^{2}+{{y}_{1}}^{2}={{c}^{2}}$ .
Hence the line is tangent to the circle ${{x}_{1}}^{2}+{{y}_{1}}^{2}={{c}^{2}}$ .
Now the center of the circle is (0, 0) and radius of the circle is c.
Now length of a line perpendicular to $ax+by+c=0$ from point $\left( {{x}_{1}},{{y}_{1}} \right)$ is given by, $\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
Hence the perpendicular distance from center of the circle is (0, 0) to the line $x{{x}_{1}}+y{{y}_{1}}={{b}^{2}}$ is given by, $\dfrac{\left| -{{b}^{2}} \right|}{\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}}$
But this distance is nothing but the radius of the circle since we know that the perpendicular drawn from the center to the tangent is nothing but radius. Hence we get,
$\dfrac{{{b}^{2}}}{\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}}=c$
Now substituting the value from equation (1) we get,
$\dfrac{{{b}^{2}}}{\sqrt{{{a}^{2}}}}=c$
Hence we get ${{b}^{2}}=ac$ .
This means b is the geometric mean of a and c.
Hence a, b and c are in GP.

Note: Note that the radius of circle is always perpendicular to tangent at any point on the circle. Hence we have the result that the perpendicular drawn from the center of the circle to the tangent is the radius of the circle.