Question

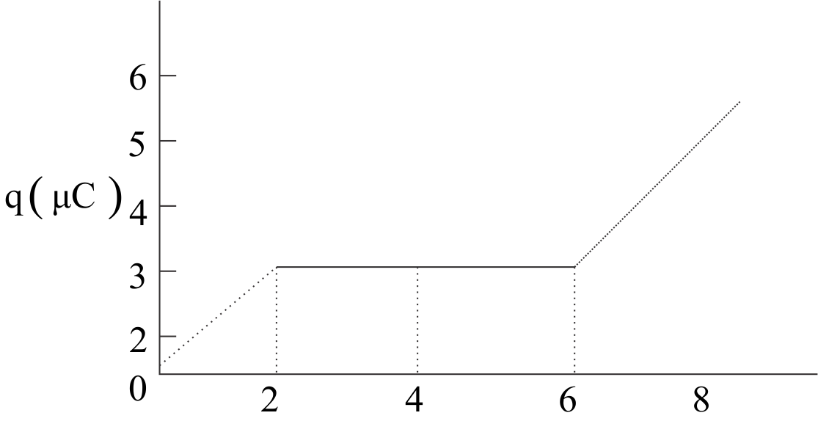
The charge on a capacitor plate in a circuit, as a function of time, is shown in the given figure. What is the value of current at t = 4 s?

A) 3 $\mu$A
B) 2 $\mu$A
C) Zero
D) 1.5 $\mu$A

Answer 1

The current flowing through the circuit is equal to the change in charge per unit time. It can be found out by finding out the slope of the graph at the required point.

Complete step by step answer: The charge on a capacitor plate is given as the function of time. Since, we have the graphical representation of the charge with respect to time, we can easily find out the rate of change of charge on the capacitor plate with respect to time.
As we see in the graph, there is a change in the slope at t = 2 s and again at t = 6 s. So, we can divide the graph into three parts. Let us name the part of the graph from t = 0 s to t = 2 s as part A, from t = 2 s to t = 6 s as part B and from t = 6 s onwards as part C.
According to the question, we need to find out the value of current at t = 4 s. So, only the slop of the graph at t = 4 s is required. In part B of the graph, the slope is constant. So, we consider part B of the graph. The graph is a straight line in part B.
We find out the slope of a straight line by using the equation,
Slope = $\dfrac{{\Delta y}}{{\Delta x}} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$ …equation (1)
In part B, at t = 2 s, q = 3 $\mu$C, and at t = 6 s, q = 3 $\mu$C. On substituting these values in equation (1), we obtain,
${\left. {\dfrac{{dq}}{{dt}}} \right|_{t = 4s}} = \dfrac{{{q_2} - {q_1}}}{{{t_2} - {t_1}}} = \dfrac{{3 - 3}}{{6 - 2}} = 0$
Hence, at t = 4 s, the current flowing in the circuit is zero.

Therefore, option C is the correct answer.

Note: The slope of the graph can also be found out by finding out the equation of the lines and then differentiating it. However, it would involve more steps, which would be unnecessary.