Question
Question: The charge (in \(\mu C\) ) on any one of the 2\(\mu F\) capacitor will be given respectively as: !...
The charge (in μC ) on any one of the 2μF capacitor will be given respectively as:
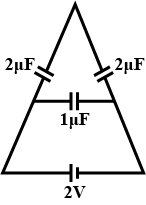
A) 1, 2
B) 2, 1
C) 1, 1
D) 2, 2
Solution
In order to find the charge we need to find the charge separately for each capacitor. Capacitors having 2μF are in series hence equal charge will be there with half of the voltage and capacitor 1μF is along 2V and have charge different to others. This is how we will get the charges on capacitors.
Step by step solution:
Step 1:
Let us know about the capacitor first before solving the question:
A capacitor (originally known as a condenser) is a passive two-terminal electrical component used to store energy electro statically in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors (plates) separated by a dielectric (i.e. insulator).
The starting capacitor works by accumulating a large electrical charge inside the capacitor. During compressor or other motor startup, the start capacitor releases its charge to give a voltage "boost" to get the electric motor spinning.
Step 2:
In question we are given that a voltage supply of 2V has been given to three capacitors of charge 2, 2, and 1 micro farad .
The two capacitors are in series with each other and hence will have equal charge along them and also the voltage supply will get distributed along them in equal amounts.
Let them have a charge of Q1 for both and the voltage will be 2V which is 1V each.
Coming to the third capacitor it has the voltage 2V and let say it has a charge of Q2
Now, for Q1 charge is equal to the product of capacitance and voltage across it .
So Q1=2μF×1V . This is equal to 2μC for each.
Coming to the third one Q2 =1μF×2V. This is equal to 2μC
Hence both Q1 and Q2 have same charge of 2μC
Option D is correct.
Additional information:
Capacitors have many important applications. They are used, for example, in digital circuits so that information stored in large computer memories is not lost during a momentary electric power failure; the electric energy stored in such capacitors maintains the information during the temporary loss of power.
Capacitors (sometimes known as condensers) are energy-storing devices that are widely used in televisions, radios, and other kinds of electronic equipment. Tune a radio into a station, take a flash photo with a digital camera, or flick the channels on your HDTV and you're making good use of capacitors.
Note:
To find the solution one must know that when capacitors are in series they possess equal charge and the voltage supply gets divided among them in equal amounts. To find the charge we need to remember one thing that charge is equal to the product of capacitance and voltage across it, and must not make mistakes in finding the voltage across capacitors.
