Question
Question: The charge and mass of two particles are \( + Q,M \) and \( - q,m \) respectively. The particles, se...
The charge and mass of two particles are +Q,M and −q,m respectively. The particles, separated by a distance L , are released from rest in a uniform electric field E . The electric field is parallel to the line joining both the charges and is directed from negative to positive charge. For the separation between the particles to remain constant, the value of L is : (K=4πεo1)
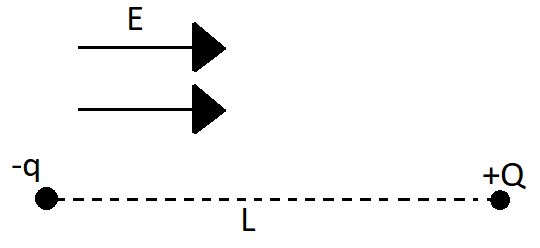
(A) E(qM+Qm)(M+m)KQq
(B) E(qm+QM)(M+m)KQq
(C) E(qM+Qm)mMKQq
(D) E(QM+qm)mMKQq
Solution
Hint
In the presence of the electric field, both the charges will experience a force on them, which is the sum of the force due to the electric field and the presence of the other charge. So we can find the equation of motion of both the particles. And for the distance between the particles to be constant, the relative acceleration of the particles in the electric field has to be zero. So from arelative=0 , that is from am=aM by substituting the values we get the required value.
Formula used: To solve this equation, we use the following formula,
F=ma , the equation of motion
where F is the force on the charged particles
m is the mass of the charged particle and a is the acceleration of the particle.
where the force is the sum of the force due to the electric field given by qE and the force due to the other charged particle given by L2KQq .
Complete step by step answer
In this question, we are given two charges, one of charge +Q and the mass M and another of charge −q and mass m . The separation of these two charges is given L and an electric field is flowing from the direction of the negative charge to the positive charge. In the presence of an electric field, both the charges will acquire an acceleration. Now for the separation between the charges to remain constant, the relative velocity between the two charges has to be constant. So we have,
vrelative=constant
∴dtd(vrelative)=0
So from the above, we get the relative acceleration as, arelative=0 since dtd(vrelative)=arelative
Now the relative acceleration is given by the difference between the acceleration between the two charges.
So, am−aM=0
The force on each of the charged particles is the sum of the force due to the electric field on the particle and the force due to the other charged particle.
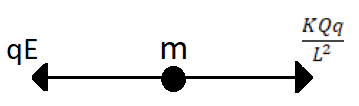
For the particle of mass m the force on it due to the electric field will be towards the left given by qE and the force due to the other charge of mass M will be attractive as the two masses are of opposite charge and is given by L2KQq towards the right.
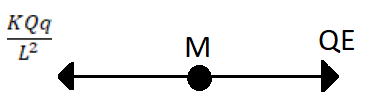
For the particle of mass M the force on it due to the electric field will be towards the right given by QE and the force due to the other charge of mass m will be L2KQq towards the left.
Now if we consider, the acceleration toward the right to be positive, then the total force on the mass m will be
Fm=−qE+L2KQq .
And from the equation of motion, this force is given by Fm=mam
∴mam=−qE+L2KQq
⇒am=−mqE+m1L2KQq
The total force on the mass M is,
FM=QE−L2KQq
And similarly, from the equation of motion, we get,
∴MaM=QE−L2KQq
⇒aM=MQE−M1L2KQq
Now the for the relative acceleration to be zero,
am−aM=0
⇒−mqE+m1L2KQq=MQE−M1L2KQq
Now by arranging the terms we get,
mqE+MQE=M1L2KQq+m1L2KQq
Now by taking common from both sides,
E(mq+MQ)=L2KQq(M1+m1) ,
Now by performing the addition of the fractions,
⇒E(MmqM+Qm)=L2KQq(MmM+m)
We can cancel Mm from the denominator of both the sides,
∴E(qM+Qm)=L2KQq(M+m)
Therefore we take L2 to the L.H.S of the equation and terms on the L.H.S. to the R.H.S, we get
∴L2=E(qM+Qm)KQq(M+m)
Now taking square root over both the sides we get
L=E(qM+Qm)(M+m)KQq
Hence the correct answer is option (A).
Note
In this question, the electric field is present in a direction from the negative charge −q to the positive charge Q . So the direction of the force due to the electric field will be different in both the cases as the charges of the two particles are opposite.
