Question

The change in current through a junction diode is $1.2mA$ when forward bias voltage is changed by $0.6V$.The dynamic resistance is

& A.500\Omega \\\ & B.300\Omega \\\ & C.150\Omega \\\ & D.250\Omega \\\ \end{aligned}$$

Answer 1

Dynamic resistance is also known as AC resistance, as typical resistance formula, it depends on change in current and voltage. Here, we take these from the operating point q in the V-I characteristics of a diode. For every small change in voltage it experienced a large change in current.

Formula used:
${{r}_{dynamic}}=\dfrac{\Delta V}{\Delta I}$

Complete answer:
As we know about resistance, it is the opposing force against flow of current. In case of a diode there are 2 types of resistances. Static and dynamic. Static resistance is the resistance when the diode is applied to DC and Dynamic resistance is the resistance offered by the diode when AC is applied. It is also known as AC resistance.
When we examine the V-I characteristics of p-n junction diode as shown in the picture,

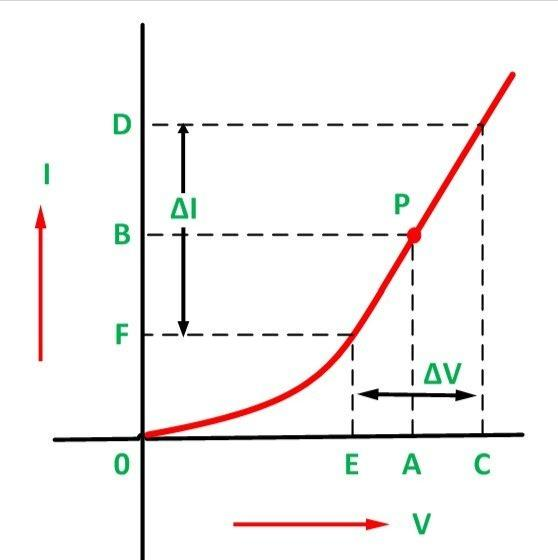
The ratio of change in voltage $\Delta V$ to the change in current $\Delta I$ represents dynamic resistance.
I.e., ${{r}_{dynamic}}=\dfrac{\Delta V}{\Delta I}$
In the question, it is given that,
Change in voltage, $\Delta V=0.6V$and Change in current,$\Delta I=1.2mV$

& \Rightarrow {{r}_{dynamic}}=\dfrac{0.6V}{1.2mA} \\\ & \\\ \end{aligned}$$ $$\begin{aligned} & {{r}_{dynamic}}=\dfrac{0.6}{1.2}\times {{10}^{3}} \\\ & {{r}_{dynamic}}=\dfrac{600}{1.2}=500\Omega \\\ & \\\ \end{aligned}$$ So, we found that the dynamic resistance of the diode at the given voltage is $$500\Omega $$ **Therefore, the correct answer is option A .** **Note:** We can also do the dynamic resistance problem only by knowing diode current too. The formula is given as, $$\begin{aligned} & \dfrac{\Delta {{V}_{d}}}{\Delta {{I}_{d}}}=\dfrac{\eta {{V}_{t}}}{{{I}_{d}}} \\\ & \Rightarrow {{r}_{d}}=\dfrac{26mV}{{{I}_{d}}} \\\ \end{aligned}$$ Here, $${{I}_{d}}$$ is the diode current and $$\eta {{V}_{t}}$$ is equal to $$26mV$$ This formula is derived from the diode current equation, $${{I}_{d}}={{I}_{s}}({{e}^{\dfrac{{{V}_{d}}}{\eta {{V}_{t}}}}}-1)$$.