Question

The centroid of an equilateral triangle is $(0,0).$ If two vertices of the triangle lie on $x + y = 2\sqrt 2 ,$ then one of them will have its coordinates
A. $(\sqrt 2 + \sqrt 6 ,\;\sqrt 2 - \sqrt 6 )$
B. $(\sqrt 2 + \sqrt 3 ,\;\sqrt 2 - \sqrt 3 )$
C. $(\sqrt 2 + \sqrt 5 ,\;\sqrt 2 - \sqrt 5 )$
D. $(\sqrt 2 ,\;\sqrt 2 )$

Answer 1

Hint : First of all draw the diagram with the given data. Apply the concepts of the centroid. Use distance formula to measure the sides of an equilateral triangle. Also, apply the altitude and the median concepts for the resultant answer.

Complete step-by-step answer :

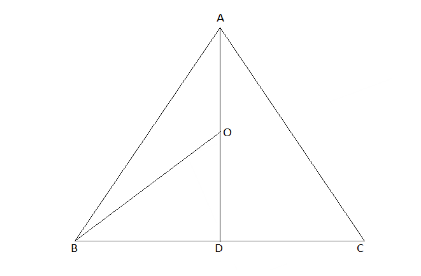
Given that the triangle is an equilateral triangle and the centroid is at $(0,0)$ . Therefore, orthocentre and incentre will lie at that point means they also will be $(0,0)$
As shown in the above figure, let us assume that the point O is the incentre of the triangle and line joining the incentre will give angle bisector.
Since, all the angles in an equilateral triangle are equal to $60^\circ$
And the angle bisector, $\angle ABO = 30^\circ$
Also, if O is the incentre of the triangle then the altitude will pass through that point and will form $90^\circ$ at point D.
Given that two vertices of the triangle lie on $x + y = 2\sqrt 2 ,$ let us assume that two vertices are at point B and point C.
Equation of BC, $x + y = 2\sqrt 2$ .... (A)
Slope of the above equation, ${m_{BC}} = ( - 1)$
Also, from the figure $OD \bot BC$
We know slopes of two perpendicular slopes is equal to $( - 1)$
${m_{BC}}.{m_{OD}} = ( - 1)$
Placing the value –
$\Rightarrow {m_{OD}} = 1$
Now, equation of line passing through $(0,0)$ is –
$y = mx$
But $m = 1$
$\Rightarrow y = x$
Equation of OD: $y = x$
Now, if we find the intersection BC at D, place $y = x{\text{ }}$ in the equation A.
$\Rightarrow x + x = 2\sqrt 2$
Simplify the above equation –
$\Rightarrow 2x = 2\sqrt 2$
Common multiples from both the sides of the equation cancel each other.
$x = \sqrt 2$ and $y = \sqrt 2$
Therefore, the co-ordinates of the point D will be $\left( {\sqrt 2 ,\sqrt 2 } \right)$
Now, $\Delta ODB = 90^\circ$ ,
$\tan 30^\circ = \dfrac{{OD}}{{BD}}$ .... (B)
From the distance formula –
$OD = \sqrt {{{(\sqrt 2 - 0)}^2} + {{(\sqrt 2 - 0)}^2}}$
Simplify the above equation –
$OD = \sqrt {2 + 2} \\\ OD = \sqrt 4 \\\ OD = 2 \\\$
Place the values in the equation (B)
$\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{2}{{BD}}$
Cross-multiply the above equation –
$\Rightarrow BD = 2\sqrt 3$ ....(C)
Now, the co-ordinates of point B which lie on $x + y = 2\sqrt 2$ is
$B = (h,2\sqrt 2 - h)$
Now, BD from the distance formula-
$BD = \sqrt {{{(h - \sqrt 2 )}^2} + {{(2\sqrt 2 - h - \sqrt 2 )}^2}}$
Place the value of BD
$\Rightarrow 2\sqrt 3 = \sqrt {{{(h - \sqrt 2 )}^2} + {{(2\sqrt 2 - h - \sqrt 2 )}^2}}$
Take square-root on both the sides of the equation –
$\Rightarrow {\left( {2\sqrt 3 } \right)^2} = {\left( {\sqrt {{{(h - \sqrt 2 )}^2} + {{(2\sqrt 2 - h - \sqrt 2 )}^2}} } \right)^2}$
Square and square cancel each other-
$\Rightarrow 12 = {(h - \sqrt 2 )^2} + {(\sqrt 2 - h)^2}$
The above equation can be re-written as –
$\Rightarrow 12 = {(h - \sqrt 2 )^2} + {(h - \sqrt 2 )^2}$
Simplify the above equation –

$$\Rightarrow 12 = 2{(h - \sqrt 2 )^2} \\\ \Rightarrow \dfrac{{12}}{2} = {(h - \sqrt 2 )^2} \\\ \Rightarrow 6 = {(h - \sqrt 2 )^2} \;$$

Take square-root on both the sides of the equation –
$\Rightarrow (h - \sqrt 2 ) = \pm \sqrt 6$
The above equation implies-
$h = \sqrt 2 - \sqrt 6 \;{\text{or }}h = \sqrt 2 + \sqrt 6$
In an equilateral triangle an altitude and the median are the same, therefore D is the midpoint of BC.
Now, the coordinates for B is
$B = (h,2\sqrt 2 - h)$
Place the values –
$B = (\sqrt 2 + \sqrt 6 ,2\sqrt 2 - \sqrt 2 - \sqrt 6 )$ or $C = (\sqrt 2 - \sqrt 6 ,2\sqrt 2 - \sqrt 2 + \sqrt 6 )$
Simplification implies –
$B = (\sqrt 2 + \sqrt 6 ,\sqrt 2 - \sqrt 6 )$ or $C = (\sqrt 2 - \sqrt 6 ,\sqrt 2 + \sqrt 6 )$
So, the correct answer is “Option A”.

Note : Follow all the steps carefully and wisely. It is lengthy but easy. Do not make silly mistakes while simplifying. Also, know the difference between the incircle and the centroid of the triangle and apply accordingly. Remember if the lines are perpendicular to each other then the product of their slopes will be equal to -1.