Question
Question: The centre of family of circles cutting the family of circles $x^2 + y^2 + 2x \left( \lambda - \frac...
The centre of family of circles cutting the family of circles x2+y2+2x(λ−23)+6y(λ−32)−8(λ+4)=0 orthogonally, lies on
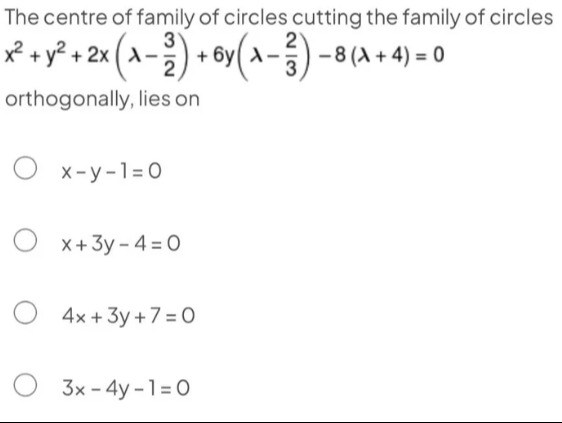
x-y-1=0
x+3y-4=0
4x+3y+7=0
3x-4y-1=0
x+3y-4=0
Solution
The given family of circles is
x2+y2+2x(λ−23)+6y(λ−32)−8(λ+4)=0.
Step 1: Expand and simplify:
Distribute the terms: 2x(λ−23)=2λx−3x,
6y(λ−32)=6λy−4y,
−8(λ+4)=−8λ−32.
Thus, the equation becomes: x2+y2−3x−4y−32+λ(2x+6y−8)=0.
Step 2: Use the radical axis method:
Consider two circles from the family corresponding to different λ values, say λ1 and λ2:
S1:x2+y2−3x−4y−32+λ1(2x+6y−8)=0,
S2:x2+y2−3x−4y−32+λ2(2x+6y−8)=0.
Subtract S2 from S1:
(S1−S2):(λ1−λ2)(2x+6y−8)=0.
Since λ1=λ2,
2x+6y−8=0.
Dividing by 2:
x+3y−4=0.
This line is the radical axis, and the centers of the circles cutting the given family orthogonally lie on this line.
