Question

The centre of a square $ABCD$ is at $z=0$. If $A$ is ${{z}_{1}}$, then the centroid of triangle $ABC$ is
A. $\dfrac{{{z}_{1}}}{3}\left( \cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2} \right)$
B. $\dfrac{{{z}_{1}}}{3}\left( \cos \pi +i\sin \pi \right)$
C. ${{z}_{1}}\left( \cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2} \right)$
D. None of these

Answer 1

Centroid of a triangle divide the median in the ratio of 2:1. If the coordinates of the vertices of the triangle are given centroid is calculated as the sum of the coordinates divided by 3. The triangle $ABC$ formed, is an isosceles triangle. We will also use the concept of rotation about the origin in a complex plane.

Complete step-by-step solution:
Let us consider the centroid of triangle $ABC$ as G. And let the center of the square $ABCD$ be O which is $z=0$.

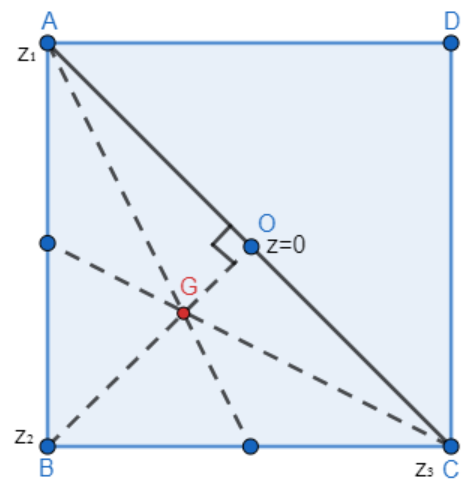
Now, in the square $ABCD$we have $OA=OB=OC$.
We have been given that, $A$ is ${{z}_{1}}$. So, let us consider $B$ as ${{z}_{2}}$ and $C$ as ${{z}_{3}}$.
So, we have, $OA={{z}_{1}}-0$, $OB={{z}_{2}}-0$ and $OC={{z}_{3}}-0$.
We know that the diagonals of a square intersect at right angles.
We will use the rotation theorem for complex numbers. If we have two complex numbers, say ${{z}_{1}}\text{ and }{{z}_{2}}$ such that $\left| {{z}_{1}} \right|=\left| {{z}_{2}} \right|$ and the angle of rotation in counter-clockwise direction from ${{z}_{2}}$ to ${{z}_{1}}$ is $\theta$ , then we can write that ${{z}_{2}}={{z}_{1}}{{e}^{i\theta }}$ .
Now, we will rotate $OA$ by right angle to $OB$ in a counter-clockwise direction. So, here we have ${{z}_{1}}=OA\text{ and }{{z}_{2}}=OB$ and $\theta ={{90}^{\circ }}=\dfrac{\pi }{2}$ . So, we can write it as
$OB=OA{{e}^{i\dfrac{\pi }{2}}}$
Now we have,
$({{z}_{2}}-0)=({{z}_{1}}-0){{e}^{i\dfrac{\pi }{2}}}$
${{z}_{2}}={{z}_{1}}{{e}^{i\dfrac{\pi }{2}}}$…………………….. (i)
Similarly, when $OA$ is rotated by ${{180}^{\circ }}$ counter-clockwise to $OC$ we can apply rotation theorem for ${{z}_{1}}=OA\text{ and }{{z}_{2}}=OC$ and $\theta ={{180}^{\circ }}=\pi$ as below,
$OC=OA{{e}^{i\pi }}$
Substituting values, we have
$({{z}_{3}}-0)=({{z}_{1}}-0){{e}^{i\pi }}$
${{z}_{3}}={{z}_{1}}{{e}^{i\pi }}$……………………… (ii)
The centroid of the triangle $ABC$ is given by G = $\dfrac{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}}{3}$ ……………. (iii)
On putting the values of ${{z}_{1}}$and ${{z}_{2}}$ from (i) and (ii) in (iii), we have
G = $\dfrac{{{z}_{1}}+{{z}_{1}}{{e}^{i\dfrac{\pi }{2}}}+{{z}_{1}}{{e}^{i\pi }}}{3}$
G = $\dfrac{{{z}_{1}}}{3}\left( 1+{{e}^{i\dfrac{\pi }{2}}}+{{e}^{i\pi }} \right)$
As we know that ${{e}^{i\theta }}=\cos \theta +i\sin \theta$, we can write G as,
G = $\dfrac{{{z}_{1}}}{3}\left( 1+\cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2}+\cos \pi +i\sin \pi \right)$
We know that $\cos \pi =-1$ and $\sin \pi =0$. So, on applying this property, we will get,
G = $\dfrac{{{z}_{1}}}{3}\left( 1+\cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2}-1+0 \right)$
On simplifying further, we will get,
G = $\dfrac{{{z}_{1}}}{3}\left( \cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2} \right)$
Hence, the centroid of the triangle $ABC$ is G = $\dfrac{{{z}_{1}}}{3}\left( \cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2} \right)$.
Therefore, option A is correct.

Note: In this question, the concept which is very much important to keep in mind is the rotation of vector in a complex plane. Don’t get confused with the angle of rotation as we have done a counter-clockwise rotation in this particular problem so we get the answer $\dfrac{{{z}_{1}}}{3}\left( \cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2} \right)$, we may have also done the rotation in a clockwise direction and in that case the answer will be $\dfrac{{{z}_{1}}}{3}\left( \cos \dfrac{\pi }{2}-i\sin \dfrac{\pi }{2} \right)$. Also, the formula for the centroid of a triangle is important to solve these types of problems.