Solveeit Logo
Login

Question

Question: The central angle of a quadrant is ______ \[\left( \text{a} \right)\text{ }{{90}^{\circ }}\] \[\...

The central angle of a quadrant is ______
(a) 90∘\left( \text{a} \right)\text{ }{{90}^{\circ }}
(b) 180∘\left( \text{b} \right)\text{ 18}{{0}^{\circ }}
(c) 270∘\left( \text{c} \right)\text{ 27}{{0}^{\circ }}
(d) 0∘\left( \text{d} \right)\text{ }{{0}^{\circ }}

Explanation

Solution

Hint : To solve the given question, we will first find out about the rectangular coordinate system in a two – dimensional plane and also we will find out about the coordinate axis and how they are placed in a rectangular coordinate system to form a quadrant. Then, we will find out the total number of quadrants and we will divide 360∘{{360}^{\circ }} by this number to get the central angle of a quadrant.

Complete step by step solution :
Before solving the question given, we must have some knowledge about the rectangular coordinate system. A rectangular coordinate system is a coordinate system that specifies each point uniquely in a plane by a set of numerical coordinates, which are the signed distances to the point from the two fixed perpendicular lines, measured in the same unit of length. In a rectangular coordinate system, there are two axes, the x-axis and the y-axis. The x-axis is the horizontal axis and the y-axis is the vertical axis. The point of intersection of these two axes is called the origin, denoted by O. The rectangular coordinate system in two dimensions is shown in the following figure.

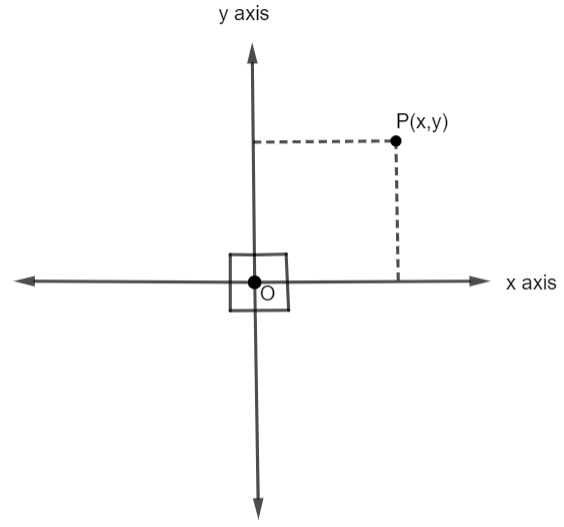
Due to the intersection of the coordinate axes, the plane is divided into four regions. This is called the quadrant region. There are a total of four quadrants in the plane. The total angle subtended at the center is 360∘.{{360}^{\circ }}. Thus, the central angle of each quadrant =360∘4=90∘.=\dfrac{{{360}^{\circ }}}{4}={{90}^{\circ }}.
Hence, option (a) is the right answer.

Note : here, we have considered the rectangular coordinate system in two dimensions only. There may be three dimensions of the system but in that case, also, there will be 8 quadrants but the central angle will still remain 90∘.{{90}^{\circ }}. Thus, no matter what kind of system we have, the central angle of a quadrant will always be 90∘.{{90}^{\circ }}.