Question

The center of a circle is (2a-1, a). Find the value of a, if the circle passes through the point (10, -2) and has diameter $10\sqrt 2$ units.

Answer 1

Hint: In this question use the distance formula that is $d = \sqrt {{{\left( {{x_1} - x} \right)}^2} + {{\left( {{y_1} - y} \right)}^2}}$ , where x, y are the general points lying on the circle that is (10, -2) in this case. So find the distance between the center of the circle and the given point of the circle, then use the concept that distance between the center and any general point on the circle is actually the radius. This will help approaching the problem.

Complete step-by-step answer:

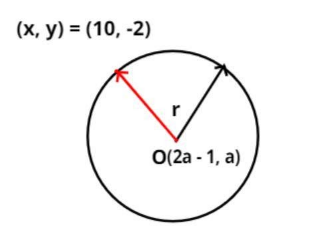
Given data:
Center of a circle is (2a – 1, a).
Circle passes through the point (10, -2).
And has diameter (D) = 10 $\sqrt 2$ units.
As we all know that the distance from the center on the circumference of the circle is nothing but the radius of the circle, as shown in the figure.
Let the point on the circumference of the circle is (x, y)
Therefore, (x, y) = (10, -2)
And let the center of the circle be $\left( {{x_1},{y_1}} \right) = \left( {2a - 1,a} \right)$
Now as we all know that the distance between the two points is given as
$d = \sqrt {{{\left( {{x_1} - x} \right)}^2} + {{\left( {{y_1} - y} \right)}^2}}$
And this distance is nothing but the radius of the circle so, d = r, where r is the radius of the circle.
Now as we all know that the radius of the circle is half of the diameter (D) of the circle.
Therefore, $r = \dfrac{D}{2} = \dfrac{{10\sqrt 2 }}{2} = 5\sqrt 2$ Units.
Therefore, $d = r = \sqrt {{{\left( {{x_1} - x} \right)}^2} + {{\left( {{y_1} - y} \right)}^2}}$
Now substitute the values in the above equation we have,
$\Rightarrow 5\sqrt 2 = \sqrt {{{\left( {2a - 1 - 10} \right)}^2} + {{\left( {a - \left( { - 2} \right)} \right)}^2}}$
Now squaring on both sides we have,
$\Rightarrow {\left( {5\sqrt 2 } \right)^2} = {\left( {\sqrt {{{\left( {2a - 1 - 10} \right)}^2} + {{\left( {a - \left( { - 2} \right)} \right)}^2}} } \right)^2}$
Now simplify this we have,
$\Rightarrow 25\left( 2 \right) = {\left( {2a - 1 - 10} \right)^2} + {\left( {a - \left( { - 2} \right)} \right)^2}$
$\Rightarrow 50 = {\left( {2a - 11} \right)^2} + {\left( {a + 2} \right)^2}$
Now open the square according to property ${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab{\text{ and }}{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$ so we have,
$\Rightarrow 50 = 4{a^2} + 121 - 44a + {a^2} + 4 + 4a$
$\Rightarrow 5{a^2} + 75 - 40a = 0$
Now divide by 5 throughout we have,
$\Rightarrow {a^2} - 8a + 15 = 0$
Now factorize this equation we have,
$\Rightarrow {a^2} - 3a - 5a + 15 = 0$
$\Rightarrow a\left( {a - 3} \right) - 5\left( {a - 3} \right) = 0$
$\Rightarrow \left( {a - 5} \right)\left( {a - 3} \right) = 0$
$\Rightarrow a = 5,3$
So this is the required value of (a) such that the circle passes through the point (10, -2) has diameter $10\sqrt 2$ units.
So this is the required answer.

Note:There is a very important criteria regarding the circle that is generally considered as the locus of points that are moving at a constant distance from a fixed point, this fixed point is considered as the center of the circle and these moving points at a constant distance are the general points on the circle called as radius, hence the distance between the centre and point (10,-2) is taken as r.