Question
Question: The cartesian equation of the plane passing through the point (0, 7, -7) and containing $\frac{x+1}{...
The cartesian equation of the plane passing through the point (0, 7, -7) and containing −3x+1=2y−3=1z+2 is
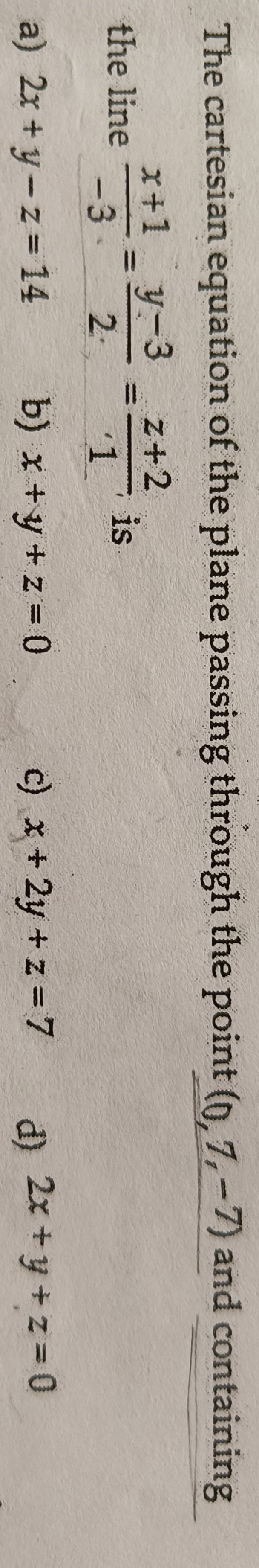
2x + y - z = 14
x + y + z = 0
x + 2y + z = 7
2x + y + z = 0
x + y + z = 0
Solution
-
Find a point on the line and its direction vector:
The line in symmetric form is
−3x+1=2y−3=1z+2=t.Thus, the parametric equations are:
x=−1−3t,y=3+2t,z=−2+t.When t=0, a point on the line is Q(−1,3,−2). The direction vector of the line is:
d=(−3,2,1). -
Determine a second vector in the plane:
The plane passes through P(0,7,−7) and contains the line. So, the vector from Q(−1,3,−2) to P(0,7,−7) is:
QP=(0−(−1),7−3,−7−(−2))=(1,4,−5). -
Find the normal vector (n) to the plane:
The normal vector is the cross product of d and QP:
n=d×QP=(−3,2,1)×(1,4,−5).Computing the cross product:
n=(2(−5)−1(4),−((−3)(−5)−1(1)),−3(4)−2(1)) =(−10−4,−(15−1),−12−2) =(−14,−14,−14).Dividing by −14 (since the equation remains unchanged if the normal vector is multiplied by a scalar), we get:
n=(1,1,1). -
Write the equation of the plane:
The plane passing through P(0,7,−7) with normal vector (1,1,1) is given by:
1(x−0)+1(y−7)+1(z+7)=0.Simplify:
x+y−7+z+7=0⇒x+y+z=0.
Answer:
Option b) x+y+z=0
Explanation (Core):
Find a point on the line Q(−1,3,−2) and direction vector d=(−3,2,1). Compute vector from Q to P(0,7,−7): (1,4,−5). Find the normal using the cross product: n=(1,1,1). Using the point-normal form, the plane equation is x+y+z=0.
