Question
Question: The cardinality of a set A is 4 and that of set B is 3, then what is the cardinality of the set \(A\...
The cardinality of a set A is 4 and that of set B is 3, then what is the cardinality of the set A△B.
A. 1
B. 5
C. 7
D. Cannot be determined
Solution
Hint: The set theory will be used to solve this problem. The cardinality of a set is defined as the number of elements in the set. For example, a set A ={1, 2, 3} has a cardinality of 3. Also, A△B represents a set which contains elements which are NOT common in A and B. We will try to find the number of elements in this set to find the answer.
Complete step-by-step answer:
We have been given a set A with cardinality 4, and a set B with a cardinality of 3. The cardinality of a set is equal to the number of elements in that set, so we can write that-
n(A) = 4
n(B) = 3
We need to find the cardinality of the set A△B. This set contains the elements present in A but not in B and those which are present in B but not in A. In other words, it contains all the elements which are NOT common in A and B. It can be represented using Venn diagram as-
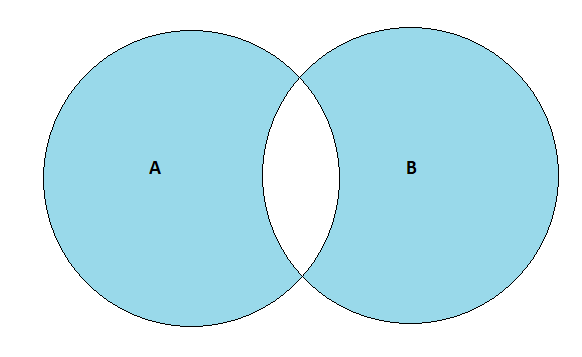
The shaded region represents A△B. Mathematically, the formula to calculate the cardinality of A△B is-
n(A△B)=n(A∪B)−n(A∩B) which is the difference of union of A and B and the intersection of A and B. But we do not know the number of elements common in A and B, so it is not possible to find the cardinality of A△B. Hence, the correct option should be D.
Note: The students should always remember that A△B, contains the elements that are not common in A and B. They often misinterpret this definition and assume that this is a set of the elements that are common in A and B. Also, whenever they encounter a problem in set theory, they should always draw a suitable Venn diagram to better understand the problem.
