Question

The capacitor shown in fig A2.11 is in steady state.

The energy stored in the capacitor is
(A) $C{I^2}{R^2}$
(B) $2C{I^2}{R^2}$
(C) $4C{I^2}{R^2}$
(D) None of these

Answer 1

R is resistor, C is capacitor and I is current flowing in wire. We will now consider wire containing capacitors as current is flowing in steady state in that branch of wire. We will find energy stored in the capacitor using $U = \dfrac{1}{2}C{V^2}$ formula where V is the potential difference across the capacitor.

Complete step by step answer

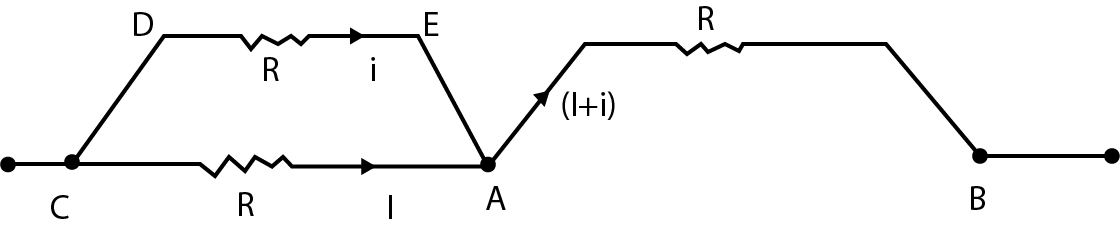
Fig A2.12.
Capacitor:
It is a two terminal device which is used to store energy in the form of an electric field. It is also known as condenser. Basically, two metallic plates are separated by a dielectric constant. S.I. unit is farad.
Resistor:
It is used to resist the flow of current. It is a passive element. S.I. unit is ohm.
Circuit:
It is a path used to conduct electricity. It consists of various elements like resistor, capacitor, wire, key, etc.

A steady state current flows through a capacitor (given). So the new circuit is as shown in fig A2.12.
Now applying loop rule or Kirchhoff’s voltage law in loop CDEAC, we get
$IR = iR$
$\Rightarrow I = i$
Now, current that flows in AB branch
$AB = I + i$
$AB = 2I$
Therefore, voltage in branch AB will be
$\Delta V = iR$
$\Delta {V_{AB}} = 2IR$
Energy stored in capacitor will be
$U = \dfrac{1}{2}C\Delta {V_{AB}}^2$
$U = \dfrac{1}{2}C{(2IR)^2}$
$U = 2C{I^2}{R^2}$

Therefore, energy stored in the capacitor is $2C{I^2}{R^2}$. So, option B is the correct
Note
If we had used energy stored formula directly without applying loop rule then instead of 2I we would have used the same current flowing in the circuit say I which is wrong. Because of which we might have got $\dfrac{{C{I^2}{R^2}}}{2}$ as our solution. But this won’t satisfy any option hence we would choose the option.