Question
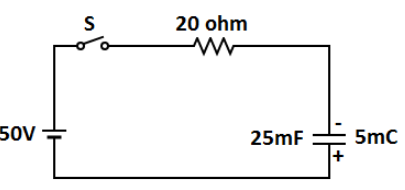
Question: The capacitor \(C\) is charged to \(5\,mC\) when the switch \(S\) in the circuit given below is kept...
The capacitor C is charged to 5mC when the switch S in the circuit given below is kept open. If at t=0sec switch S is closed, the variation of potential drop VR across the resistance 20Ω with time is represented by:
Solution
In the given circuit, the capacitor will get charged with time and firstly we will find the charge on the capacitor at a particular time and then we will find the charging and discharging current which is time derivative of charge variable.
Complete step by step answer:
Let us convert the initial charge of capacitor into coulomb.5mc=5×10−3C And let q(t) be the charge varies with time and value of RC1=2000sec
q(t)=2001e−2000t
Now we also know that,
Discharging current can be written as i(t)=dtdq(t)
i(t)=−10e−2000t→(i)
Since, for charging the capacitor, the current with time is written as
q−VCdq=−RC1dt
⇒ln(q−VC)=−RC1t+lnK
Since at time equals to zero this charge q=0 hence,
q(t)=1.25×10−3(1−e−2000t)
differentiating above equation with respect to time, we will get the current as:
i(t)=6.25×10−3×2×e−2000t
⇒i(t)=12.50e−2000tA
∴VR(t)=250e−2000tV
Now, we have the value of voltage and the current. Now, we can draw a graph between voltage versus time keeping voltage in Y-direction and time on X-direction. So the graph can be represented as:
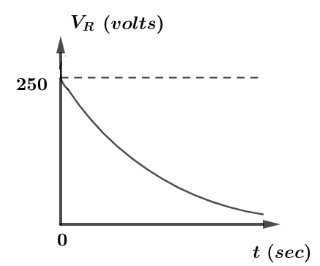
Hence, above is the variation between voltages across the resistor with time.
Note: It should be remembered that, the negative of Euler constant with a negative exponent is a decreasing graph with dependent variable while Euler constant having a positive exponent has an increasing graph with dependent variable and hence, in this case Euler constant has a negative slope.
