Question
Question: The capacitor 1 has an initial charge $Q_0$ and capacitor 2 is initially uncharged. The switch is cl...
The capacitor 1 has an initial charge Q0 and capacitor 2 is initially uncharged. The switch is closed at
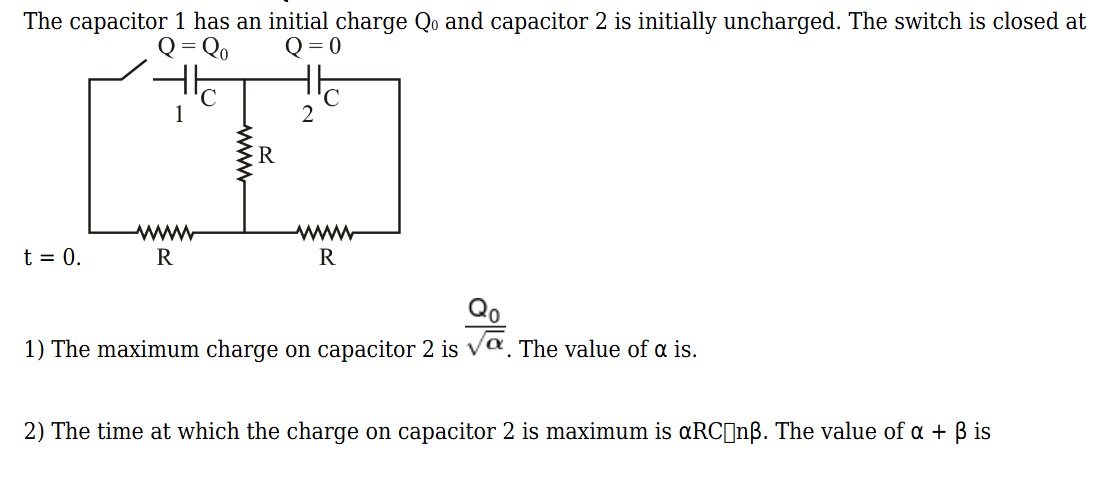
27
9
3
1
27
Solution
Here's how to solve this problem:
1. Setting up the Equations
By writing the (linear) equations for the two “nodes” at the bottom ends of the two capacitors – each of which is connected by a resistor R to a fixed (common) “ground” node – and with the two bottom‐nodes further joined by a resistor R, the problem becomes equivalent to solving:
dV₁/dt = –(2V₁ – V₂)/(RC) dV₂/dt = –(2V₂ – V₁)/(RC)
with the initial conditions:
V₁(0) = Q₀/C and V₂(0) = 0
Here V₁ and V₂ are the voltages (with the sign chosen so that a capacitor’s charge is Q = C·(voltage across it)). (This “bottom‐node” formulation is the natural one when each capacitor “has its own” resistor in series at the bottom; the resistor joining the two bottom nodes gives the extra coupling.)
2. Diagonalizing the System
One diagonalizes the 2×2 system. In matrix‑form one must solve:
d/dt [V₁; V₂] = –(1/(RC)) [2 –1; –1 2] [V₁; V₂].
The eigen‐values of the symmetric matrix are λ₁ = 1 and λ₂ = 3 (in units of 1/(RC)). Hence one may show that the solution may be written as:
V₁(t) = (Q₀/(2C)) [e^(–t/(RC)) + e^(–3t/(RC))] and V₂(t) = (Q₀/(2C)) [e^(–t/(RC)) – e^(–3t/(RC))].
Since the capacitor charges are Q₁ = C V₁ and Q₂ = C V₂ the initially uncharged capacitor (number 2) gets:
Q₂(t) = (Q₀/2)[e^(–t/(RC)) – e^(–3t/(RC))].
3. Finding the Maximum Charge
To find the maximum of Q₂(t) we set its time‐derivative equal to zero; one finds:
–(1/(RC)) e^(–t/(RC)) + (3/(RC))e^(–3t/(RC)) = 0 e^(–2t/(RC)) = 1/3 ⟹ t_max = (RC/2) ln 3.
Thus the maximum charge on capacitor 2 is:
Q₂(max) = (Q₀/2)[3^(–½) – 3^(–3/2)] = Q₀ · (3^(–3/2)); that is, Q₂(max) = Q₀/(3√3).
4. Determining α
Now the problem is stated in the following way. It is said that the maximum charge on capacitor 2 is:
Q₀/√(α).
Hence, one must have:
Q₀/√(α) = Q₀/(3√3) ⟹ √(α) = 3√3 ⟹ α = 27.
Therefore, the value of α in the maximum–charge expression is 27.
