Question

The capacitance of two concentric spherical shells of radii ${R_1}$ and ${R_2}$ $\left( {{R_2} > {R_1}} \right)$ is:
(A) $4\pi {\varepsilon _0}{R_2}$
(B) $4\pi {\varepsilon _0}\dfrac{{{R_2} - {R_1}}}{{{R_1}{R_2}}}$
(C) $4\pi {\varepsilon _0}\dfrac{{{R_1}{R_2}}}{{{R_2} - {R_1}}}$
(D) $4\pi {\varepsilon _0}{R_1}$

Answer 1

To solve this question, we need to consider a charge on the system of spherical shells. Then we have to find out the potential difference in the system with the help of the charge distribution in the system. Finally, we have to apply the basic formula of the capacitance to get the final answer.

Formula used: The formulae which are used to solve this question are given by
$\Rightarrow V = \dfrac{Q}{{4\pi {\varepsilon _0}R}}$, here $V$ is the potential on a sphere of radius $R$ which has a charge of $Q$.
$\Rightarrow C = \dfrac{Q}{V}$, here $C$ is the capacitance, $Q$ is the charge, and $V$ is the potential difference.

Complete step by step answer
Let us consider the two spherical shells of radii ${R_1}$ and ${R_2}$ as shown in the figure below. Let the outer sphere be charged with a charge of $+ Q$. The charge will get distributed on the whole surface of the outer spherical shell.

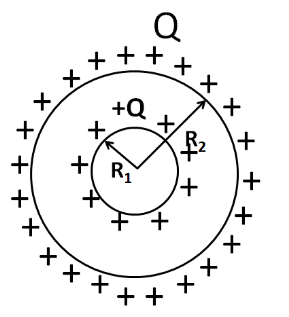
Due to the positive charge on the outer sphere, an equal amount of positive charge will appear at the outer surface of the inner sphere, as shown in the figure below.

So the potential of the outer spherical shell becomes
$\Rightarrow {V_1} = \dfrac{Q}{{4\pi {\varepsilon _0}{R_2}}}$ ………………….(1)
Also the potential of the inner spherical shell is
$\Rightarrow {V_2} = \dfrac{Q}{{4\pi {\varepsilon _0}{R_1}}}$ ………………………….(2)
So the net potential difference between the two spherical shells is
$\Rightarrow V = {V_2} - {V_1}$
From (1) and (2)
$\Rightarrow V = \dfrac{Q}{{4\pi {\varepsilon _0}{R_1}}} - \dfrac{Q}{{4\pi {\varepsilon _0}{R_2}}}$
$\Rightarrow V = \dfrac{Q}{{4\pi {\varepsilon _0}}}\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
On simplifying we get
$\Rightarrow V = \dfrac{{Q\left( {{R_2} - {R_1}} \right)}}{{4\pi {\varepsilon _0}{R_1}{R_2}}}$ ……………(3)
Now we know that the capacitance is given by
$\Rightarrow C = \dfrac{Q}{V}$
Substituting (3) we have
$\Rightarrow C = \dfrac{Q}{{\dfrac{{Q\left( {{R_2} - {R_1}} \right)}}{{4\pi {\varepsilon _0}{R_1}{R_2}}}}}$
On simplifying, we finally get
$\Rightarrow C = 4\pi {\varepsilon _0}\dfrac{{{R_1}{R_2}}}{{{R_2} - {R_1}}}$
Thus, the capacitance of the given two concentric spherical shells is equal to $4\pi {\varepsilon _0}\dfrac{{{R_1}{R_2}}}{{{R_2} - {R_1}}}$.

Hence, the correct answer is option C.

Note
This question could also be attempted by considering the electric field at an arbitrary point between the two spherical shells to find out the net potential difference. Then applying the formula for the capacitance as above will give the final answer.