Question

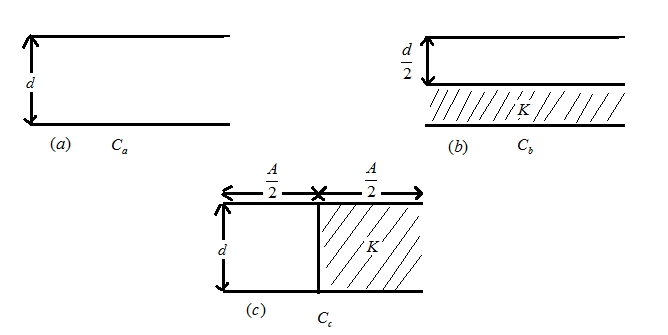
The capacitance of the parallel plate capacitor is ${C_a}$ (figure). A dielectric of dielectric constant $K$ is inserted as shown in figure. If ${C_b}$ and ${C_c}$ denote that the capacitances in figure, then:
(A) Both ${C_b},{C_c} > {C_a}$
(B) ${C_c} > {C_a}$ while ${C_b} > {C_a}$
(C) Both ${C_b},{C_c} < {C_a}$
(D) ${C_a} = {C_b} = {C_c}$

Answer 1

Hint : Here, we have to derive the capacitances of all the given capacitors as shown in the figure. By using formulas for capacitance, effective capacitance in series and parallel combination of capacitors. And finally a comparison between them.

Complete Step By Step Answer:
let us consider the given data in the form of figures $(a),(b)\& (c)$
Thus, we have to solve these figures one by one.
Let us consider figure $(a)$ first
For $(a)$ , we have distance between to plates of capacitor as $d$ and the area is given by $A$
Thus, the capacitance ${C_a}$ is given by
${C_a} = \dfrac{{A{\varepsilon _0}}}{d}$ …. (Have no dielectric) $(1)$
Similarly for figure $(b)$ the capacitor is divided into two equal parts horizontally upper part has no dielectric while lower part is filled with dielectric $K$ as shown in figure above.
Thus, we have here two capacitors in series combination, we have to find the effective capacitance of these two capacitors with the gap of $\dfrac{d}{2}$ between each plate. The capacitance is given by
Let upper part be ${C_1}$ and lower part be ${C_2}$ (with dielectric)
${C_1} = \dfrac{{A{\varepsilon _0}}}{{\dfrac{d}{2}}} = \dfrac{{2A{\varepsilon _0}}}{d}$ And ${C_2} = \dfrac{{2KA{\varepsilon _0}}}{d}$
Therefore, the effective capacitance of these capacitors in series combination is given by
${C_b} = \dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}}$
$\Rightarrow {C_b} = \dfrac{{\dfrac{{2A{\varepsilon _0}}}{d}\dfrac{{2KA{\varepsilon _0}}}{d}}}{{\dfrac{{2A{\varepsilon _0}}}{d} + \dfrac{{2KA{\varepsilon _0}}}{d}}}$
$\Rightarrow {C_b} = \dfrac{{2AK{\varepsilon _0}}}{{d\left( {1 + K} \right)}}$
$\Rightarrow {C_b} = \dfrac{{2{C_a}}}{{1 + K}}$ …. $(2)$
Again for figure $(c)$ , here area of the capacitor is divided between two parts such that the resulting capacitors are in parallel let first half be ${C_1}$ and second half with dielectric be ${C_2}$ , the gap between two parallel plates is $d$ .
${C_1} = \dfrac{{\dfrac{A}{2}{\varepsilon _0}}}{d} = \dfrac{{A{\varepsilon _0}}}{{2d}}$ and ${C_2} = \dfrac{{KA{\varepsilon _0}}}{{2d}}$
Hence, the effective capacitance of ${C_c}$ for parallel combination is given by
${C_c} = {C_1} + {C_2}$
$\Rightarrow {C_c} = \dfrac{{A{\varepsilon _0}}}{{2d}} + \dfrac{{KA{\varepsilon _0}}}{{2d}}$
$\Rightarrow {C_c} = \dfrac{{A{\varepsilon _0}}}{{2d}}\left( {1 + K} \right)$
$\Rightarrow {C_c} = \dfrac{{{C_a}}}{2}\left( {1 + K} \right)$ …. $(3)$
Thus, we conclude from the above equations $(1)$ , $(2)$ and $(3)$ that
${C_b},{C_c} < {C_a}$ …. (because $K > 1$ )
The correct answer is option A.

Note :
Here, we have been given the capacitors and with our observation we have had to find how these capacitors differ with the help of figures given. Also, using the formulas mentioned above we conclude that the ${C_b},{C_c} < {C_a}$ since $K > 1$ , the dielectric constant must be positive as we do not want negative values of charging in capacitor or capacitance of a capacitor. Negative value means discharging.