Solveeit Logo
Login

Question

Question: The capacitance between adjacent plates shown in Fig \(20.95(a)\) is 50 nF. A \(1\mu C\) charge is p...

The capacitance between adjacent plates shown in Fig 20.95(a)20.95(a) is 50 nF. A 1μC1\mu C charge is placed on the middle plate. Find the charge on the outer surface of upper plate and the potential difference between upper and middle plates:

A. 0.5μC,10V0.5\mu C,10V
B. 1μC,20V1\mu C,20V
C. 0.5μC,20V0.5 \mu C, 20 V
D. 1.0μ,40V1.0\mu ,40V

Explanation

Solution

Solution: Hint: To solve such questions, we must understand the fundamental concept of how a capacitor works. Moreover, we must also predict how the system will react in the presence of an extra charge placed within the system. We should apply the electric field equation to calculate the electric field present in the plate P.

Complete step by step answer:
We can clearly see the distribution of charge in the plates from the diagram given below. From the given diagram, we can determine that,

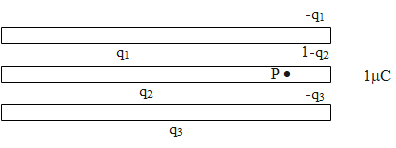
As the electric field inside the plate at p is 12Aϵ0[−q1+q+1−q2−q2+q3−q3]=0\dfrac{1}{2A{{\epsilon}_{0}}}\left[-{{q}_{1}}+q+1-{{q}_{2}}-{{q}_{2}}+{{q}_{3}}-{{q}_{3}} \right]=0
or 2q2=1⇒q2=0.5μC2 \mathrm{q}_{2}=1 \Rightarrow \mathrm{q}_{2}=0.5 \mu \mathrm{C}
Here we note that,
q1=−(1−q2)=−(1−0.5)=−0.5μCq_{1}=-\left(1-q_{2}\right)=-(1-0.5)=-0.5 \mu C
Thus, we can calculate the charge on the outer surface of the upper plate as −q1=0.5μC-q_{1}=0.5 \mu C.
Therefore, the potential difference between upper and middle plates is observed to be V=q1V=0.5×10−650×10−9=10V\text{V}=\dfrac{{{q}_{1}}}{\text{V}}=\dfrac{0.5\times {{10}^{-6}}}{50\times {{10}^{-9}}}=10\text{V}.

Hence, the correct answer is Option A.

Note: Long before batteries, capacitors were used to store charge. Even nowadays, capacitors are a better alternative to batteries because of ease in control of the charge flow. Capacitors tend to discharge quickly which is its greatest disadvantage.