Question

The cable of a uniformly loaded suspension bridge hangs in the form of parabola. The roadway which is horizontal and $100m$ long is supported by vertical wires attached to the cable, the longest wire being $30m$ and the shortest wire being $6m$ . Find the length of a supporting wire attached to the roadway $18m$ from the middle.

Answer 1

Hint : In the given question, we are given a situation where the cable of a uniformly loaded suspension bridge hangs in the form of parabola. The length of roadway is provided to us in the question. We are to find the length of supporting wire attached to the roadway $18m$ from the middle when we are given the lengths of longest as well as shortest supporting wire. The question involves the understanding of conic sections and their properties.

Complete step by step solution:
In the question, we are given a bridge whose cable is in the form of a parabola.
Now, length of roadway $= 100m$
Length of longest wire $= 30m$
Length of shortest wire $= 6m$
Now, we can see the pictorial representation of the scenario in the figure below.

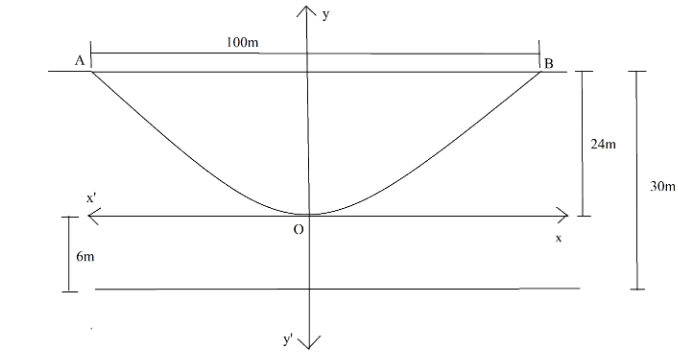
Since the parabola formed by the cable is upward facing. So, the parabola is of the form ${x^2} = 4ay$ . The axis of such parabola is the y-axis. Now, we know that the parabola is symmetrical about the axis of the parabola. So, the parabola is symmetrical about the y-axis.
So, we consider the vertex as origin and provide coordinates to other points accordingly.
So, coordinates of point B are $\left( {50,24} \right)$ . Now, point B lies on the parabola. Hence, we put the coordinates $\left( {50,24} \right)$ . So, we get,
${50^2} = 4a\left( {24} \right)$
$\Rightarrow 2500 = 4a\left( {24} \right)$
Transposing all the terms except a to left side of the equation in order to find the value of a, we get,
$\Rightarrow a = \dfrac{{2500}}{{96}}$
Cancelling common factors in numerator and denominator, we get,
$\Rightarrow a = \dfrac{{625}}{{24}}$
So, we get the value of a as $\dfrac{{625}}{{24}}$ . Now, we get the equation of parabola as ${x^2} = \left( {\dfrac{{625}}{6}} \right)y$ .
Now, we have to find the length of supporting wire attached to the roadway $18m$ from the middle. So, we can first find the coordinates of the point on parabola that is $18m$ from the middle and then find the length of the wire by adding $6m$ to the y coordinate of the point as the length of wire is to be calculated from the base.
So, finding the coordinates of the point lying on the parabola by putting x as $18m$ in the equation of parabola, we get,
${18^2} = \left( {\dfrac{{625}}{6}} \right)y$
Shifting all the terms to left side of the equation, we get the value of y as
$\Rightarrow y = 324 \times \dfrac{6}{{625}}$
We know that the square of $18$ is $324$ . Now, simplifying the calculations, we get,
$\Rightarrow y = \dfrac{{1944}}{{625}}$
$\Rightarrow y = 3.11$
Hence, length of the wire attached to the roadway $18m$ from the middle $= \left( {3.11 + 6} \right)m$
$= 9.11\,m$
Therefore, the length of the wire attached to the roadway $18m$ from the middle is $9.11\,m$.
So, the correct answer is “$9.11\,m$”.

Note : Such questions require basic knowledge of the properties of conic sections. Algebraic rules and simplification techniques are also of significant use. Care should be taken while doing calculative steps.