Question
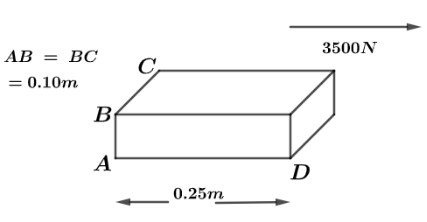
Question: The brick shown in the diagram is glued to the floor. A \(3500\,N\) force is applied to the top surf...
The brick shown in the diagram is glued to the floor. A 3500N force is applied to the top surface of the brick as shown in the figure. If the brick has shear modulus of 5.4×109Nm−2 , how far to the right does the top face move relative to the stationary bottom face?
A. 5.8×10−6m
B. 2.6×10−6m
C. 1.1×10−6m
D. 6.5×10−7m
Solution
In order to solve this question, we will use the formula of shear modulus which is defined as the ratio of pressure and relative change in length of a material.Shear Modulus of elasticity is one of the measures of mechanical properties of solids. Other elastic moduli are Young’s modulus and bulk modulus.
Formula used:
Shear modulus denoted by,
S=AF×Δxx
where, Δx is the change in length from its initial length x.
Complete step by step answer:
Let us first find the area of the cross section which is given by multiplication of sides AD and AB .
A=0.25×0.10m2
Given that, force is applied of magnitude F=3500N
And original length of sectional area is given as AD, x=0.25m
Now, we will use the formula of shear modulus to find the value of Δx .
Magnitude of shear modulus is given by S=5.4×109Nm−2
Putting these values in formula S=AF×Δxx
Δx=ASFx
⇒Δx=5.4×109×0.25×0.103500×0.25m
∴Δx=6.5×10−7m
So, change in length became Δx=6.5×10−7m
Hence, the correct option is D.
Note: Theoretically, shear modulus can be understood as simply of how much shear stress needed to make a change in shear strain which is the ratio of stress and strain. It deforms the material into a new shape which is due to shear stress applied to its cross sectional areas. Its SI unit is simple as of Pressure given by Nm−2 .
