Question

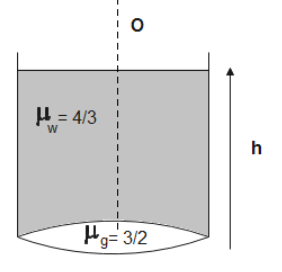
The bottom of a glass beaker is made of a thin equiconvex lens convex lens having bottom side silver polished as shown in the fig. Now water is filled in the beaker upto a height of $h=4\,m$. The image of a point object floating at the middle point of the beaker at the surface of water coincides with it. Find the value of radius (in$m$) of the curvat\ure of the lens.
${}_{a}{{\mu }_{g}}=\dfrac{3}{2},\,{}_{a}{{\mu }_{w}}=\dfrac{4}{3}$

Answer 1

The light travels through water before it reaches the lens, therefore the refractive index of lens will change with respect to water. Since the lens is silvered at the bottom, it will act like a concave mirror. We calculate the focal length of lens, mirror and lens-mirror combination in terms of radius of curvature. The image and object coincides, this means that the object is kept at radius of curvature of lens-mirror combination.
Formulas Used:
$\dfrac{1}{{{f}_{l}}}=\left( {}_{w}{{\mu }_{g}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
$R'=2f'$

Complete answer:

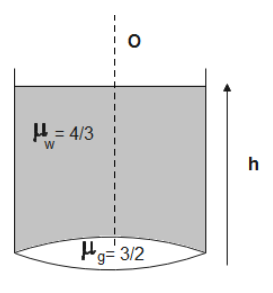
Given, the object is on the surface of water, therefore, its distance from the lens is$4\,m$
The bottom part of the lens is silvered so it will act like a concave mirror.
The focal length of the lens,${{f}_{l}}$is given by-
$\dfrac{1}{{{f}_{l}}}=\left( {}_{w}{{\mu }_{g}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
Here, ${}_{w}{{\mu }_{g}}$is the refractive index of glass with respect to water
${{R}_{1}}$is the radius of first curved surface
${{R}_{2}}$is the radius of second curved surface
Let$R$be the radius of curvature of the lens
Substituting values in the above equation, we get,

& \dfrac{1}{{{f}_{l}}}=\left( \dfrac{{{\mu }_{g}}}{{{\mu }_{w}}}-1 \right)\left( \dfrac{2}{R} \right) \\\ & \dfrac{1}{{{f}_{l}}}=\left( \dfrac{3}{2}\times \dfrac{3}{4}-1 \right)\left( \dfrac{2}{R} \right) \\\ & \Rightarrow \dfrac{1}{{{f}_{l}}}=\left( \dfrac{9}{8}-1 \right)\left( \dfrac{2}{R} \right) \\\ & \dfrac{1}{{{f}_{l}}}=\dfrac{1}{4R} \\\ \end{aligned}$$ $$\therefore {{f}_{l}}=4R$$ - (1) The focal length,$${{f}_{m}}$$ of the mirror (silvered surface) is given by- $${{f}_{m}}=\dfrac{R}{2}$$ - (2) The focal length,$$f'$$of a lens mirror combination is given by- $$\dfrac{1}{f'}=\dfrac{1}{{{f}_{m}}}+\dfrac{2}{{{f}_{l}}}$$ Substituting values from eq (1) and eq (2), we get, $$\begin{aligned} & \dfrac{1}{f'}=\dfrac{2}{R}+\dfrac{2}{4R} \\\ & \dfrac{1}{f'}=\dfrac{5}{2R} \\\ \end{aligned}$$ $$f'=\dfrac{2R}{5}$$ - (3) Given, the final image coincides with the object at $$4\,m$$, this means that the object is kept at radius of curvature of the lens mirror combination,$$R'$$. We know that, $$R'=2f'$$ $$\begin{aligned} & \Rightarrow 4=2\left( \dfrac{2R}{5} \right) \\\ & \therefore R=5\,m \\\ \end{aligned}$$ Therefore the radius of curvature of the lens is $$5\,m$$. **Note:** The value of focal lengths in the formula for focal length of lens mirror combination is taken positive for converging mirrors and lenses and negative for diverging lenses and mirrors. Concave mirror and convex lens are converging while convex mirror and concave lens are diverging. The refractive index of a medium is different when taken with respect to different mediums.