Question

The $\bot$ distance of a corner of a unit cube on a diagonal not passing through is
A. $\dfrac{{\sqrt 6 }}{3}$
B. $3\sqrt 3$
C. $2\sqrt 3$
D. None of these

Answer 1

First we will first assume that the edges OA, OB, OC of a unit cube represents the unit vectors ${\mathbf{i}}$, ${\mathbf{j}}$, ${\mathbf{k}}$ respectively and CM be the perpendicular from corner C on the diagonal OP to make a diagram. Then we will find the magnitude of the line segment OP using the formula $\sqrt {{a^2} + {b^2} + {c^2}}$, where $a$, $b$, and $c$ represents the coefficients of the unit vectors ${\mathbf{i}}$, ${\mathbf{j}}$, ${\mathbf{k}}$ respectively to find the unit vector in the direction of $\left| {\overrightarrow {{\text{OP}}} } \right|$ and then use the Pythagorean theorem ${h^2} = {a^2} + {b^2}$, where $h$ is the hypotenuse, $a$ is the height and $b$ is the base of the right-angled triangle to find the required value.

Complete step by step answer:

Let us assume that the edges OA, OB, OC of a unit cube represents the unit vectors ${\mathbf{i}}$, ${\mathbf{j}}$, ${\mathbf{k}}$ respectively.

Let CM be the perpendicular from corner C on the diagonal OP.

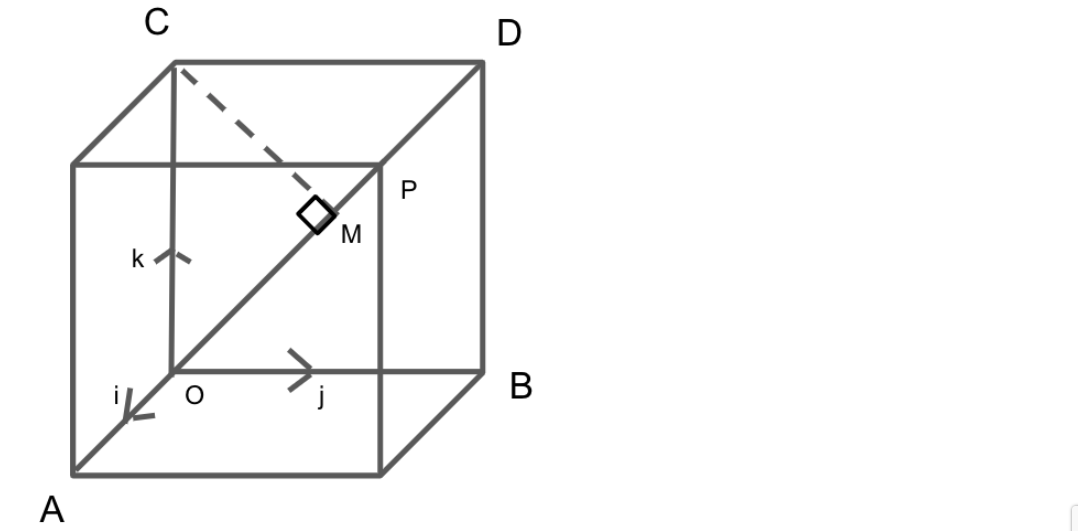
Then, since it is a unit cube we have the line segment is $\overrightarrow {{\text{OP}}} = {\mathbf{i}} + {\mathbf{j}} + {\mathbf{k}}$.

Finding the magnitude of the line segment OP using the formula $\sqrt {{a^2} + {b^2} + {c^2}}$, where $a$, $b$, and $c$ represents the coefficients of the unit vectors ${\mathbf{i}}$, ${\mathbf{j}}$, ${\mathbf{k}}$ respectively, we get

$$\Rightarrow \left| {\overrightarrow {{\text{OP}}} } \right| = \sqrt {{1^2} + {1^2} + {1^2}} \\\ \Rightarrow \left| {\overrightarrow {{\text{OP}}} } \right| = \sqrt {1 + 1 + 1} \\\ \Rightarrow \left| {\overrightarrow {{\text{OP}}} } \right| = \sqrt 3 \\\$$

Dividing the line segment by OP by its magnitude the find the unit vector in the direction of$\left| {\overrightarrow {{\text{OP}}} } \right|$, we get

$\Rightarrow \dfrac{{{\mathbf{i}} + {\mathbf{j}} + {\mathbf{k}}}}{{\sqrt 3 }}$

We know that when the diagonals intersect each other in a square, that is, the line segment OM is the projection of side of the square OC on OP from the given diagram, then we have
${\text{OM}} = \overrightarrow {{\text{OC}}} \cdot \left( {{\text{unit vector along }}\overrightarrow {{\text{OP}}} } \right)$.

Substituting the value of OC and the above unit vector along $\left| {\overrightarrow {{\text{OP}}} } \right|$ in the above equation, we get

$$\Rightarrow {\text{OM}} = {\mathbf{j}} \cdot \left( {\dfrac{{{\mathbf{i}} + {\mathbf{j}} + {\mathbf{k}}}}{{\sqrt 3 }}} \right) \\\ \Rightarrow {\text{OM}} = 0 + \dfrac{1}{{\sqrt 3 }} + 0 \\\ \Rightarrow {\text{OM}} = \dfrac{1}{{\sqrt 3 }} \\\$$

We will use the Pythagorean theorem ${h^2} = {a^2} + {b^2}$, where $h$ is the hypotenuse, $a$ is the height and $b$ is the base of the right-angled triangle.

Applying the Pythagorean theorem in the triangle OCM in the above figure, we get

$$\Rightarrow {\text{O}}{{\text{C}}^2} = {\text{C}}{{\text{M}}^2} + {\text{O}}{{\text{M}}^2} \\\ \Rightarrow {1^2} = {\text{C}}{{\text{M}}^2} + {\left( {\dfrac{1}{{\sqrt 3 }}} \right)^2} \\\ \Rightarrow 1 = {\text{C}}{{\text{M}}^2} + \dfrac{1}{3} \\\$$

Subtracting the above equation by $\dfrac{1}{3}$ on each of the sides, we get

$$\Rightarrow 1 - \dfrac{1}{3} = {\text{C}}{{\text{M}}^2} \\\ \Rightarrow \dfrac{{3 - 1}}{3} = {\text{C}}{{\text{M}}^2} \\\ \Rightarrow {\text{C}}{{\text{M}}^2} = \dfrac{2}{3} \\\$$

Taking the square root on both sides in the above equation, we get

$\Rightarrow {\text{CM}} = \pm \sqrt {\dfrac{2}{3}}$

Since the side can never be negative, the negative value of ${\text{CM}}$ is discarded.

So, the perpendicular distance is $\sqrt {\dfrac{2}{3}}$.

Since options A, B and C do not match with the final answer, so option D is correct.

Note: In solving these types of questions, students should make a diagram for better understanding and label the vertices properly to avoid confusion. One should know that the magnitude of a vector is the length of a line segment and the vector, which has a magnitude 1 is known as the unit vector. Do not use the line segment OP instead of finding the unit vector of OP.