Question

The bob of a stationary pendulum is given a sharp hit to impart a horizontal speed of $\sqrt {3gl}$ . Find the angle rotated by the thing before it becomes slack.

Answer 1

Hint : Finding out the angle at which the slacked string rotates before falling down and subtracting it from the total angle of rotation of the bob, that is pi radians, will give us the angle the string rotates before slacking. Then using the formula of the law of conservation of energy and the relation between the centripetal force and mass of bob, we can find out the correct answer.
Law of Conservation of Energy: $\sum {} (\dfrac{1}{2}m{v^2} + mgh) = 0$
Where $m$ is the mass of the bob and is expressed in kilograms $(kg)$ , $v$ is the velocity of the bob and is expressed in meters per second $(m/s)$ , $g$ is the acceleration due to gravity and is expressed in meters per second square $(m/{s^2})$ and $h$ is the height traveled by the bob and is expressed in meters $(m)$ .
Relation between centripetal force and mass of bob: $mg\cos \theta = \dfrac{{m{v^2}}}{l}$
Where $l$ is the length of the string and is expressed in meters $(m)$ .

Complete Step By Step Answer:

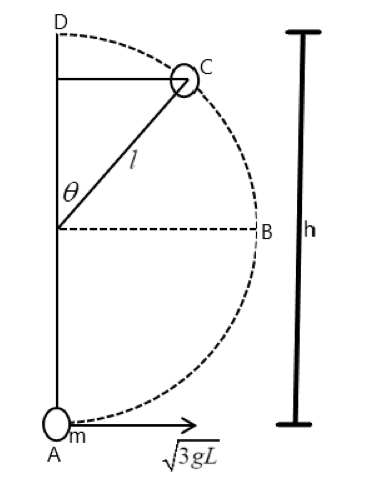
Observe the figure above,
From A to B: string is in complete tension and moving with a velocity with which it was pushed forward. Here there is a pure conversion of potential energy to kinetic energy.
From B to C: string starts to slack but not completely slacked. Here we get a gravitational potential force acting along with the kinetic energy.
From C to D: string has completely slacked. From here the string starts falling down.
Let’s assume the following quantities,
Length of string
Angle rotated by the slacked string $= \theta$
Total angle rotated by the string before falling down $= 180^\circ$
Height covered by string before completely losing tension
Velocity at point C
We know from the question,
Speed with which string is released $= \sqrt {3gl}$
Now applying law of conservation of energy from A to C,
Energy at point A= Energy at point C
Kinetic energy at A= Kinetic energy at C + Gravitational potential energy on bob at C
$\dfrac{1}{2}m{(\sqrt {3gl} )^2} = \dfrac{1}{2}m{v^2} + mg(lengthofstringfromAtoB + lengthofstringfromBtoC)$
But, the length of string from B to C $= l\cos \theta$ .
Therefore,
$\dfrac{1}{2}m{(\sqrt {3gl} )^2} = \dfrac{1}{2}m{v^2} + mg(l + l\cos \theta )$
Simplifying this we get,
$v = (gl - 2gl\cos \theta )m/s$
For the slacked string,

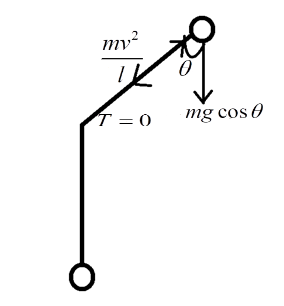
When the string is slacked, the tension $T$ in it is equal to zero. At this moment, centripetal force acts on it which pulls it inwards. This force is provided by the gravitation weight of the bob.
$mg\cos \theta = \dfrac{{m{v^2}}}{l}$
Rearranging we get,
${v^2} = gl\cos \theta$
Equating the two values of velocity at B we get,
$\cos \theta = 1/3$
But we need $\theta$ in order to find the angle traveled by the string before getting slacked.
Therefore,
$\theta = {\cos ^{ - 1}}(1/3)$
And finally,
Angle traveled by string before getting slacked $= 180 - {\cos ^{ - 1}}(1/3) = \pi - {\cos ^{ - 1}}(1/3)$ .
But $\pi \cos \theta = \cos ( - \theta )$
Therefore, the angle rotated by the thing before it becomes slack ${\cos ^{ - 1}}( - 1/3)$ .

Note :
At A, the bob is at rest so only pure kinetic energy acts on it. And from A to D, the bob is in motion so gravitational potential energy and kinetic energy both start acting on it, the kinetic energy of the bob increases and potential energy decreases. Therefore, it should be carefully equated when writing it down.