Question

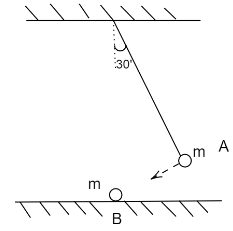
The bob of a pendulum released from ${30^ \circ }$ to the vertical hits another bob $B$ of the same mass at rest on the table as shown in the figure below. How high does the bob $A$ rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.

Answer 1

Apply law of conservation of momentum –The momentum that characterizes the motion of an isolated system remains constant. The total momentum of a system remains constant in any interaction if no external force is acted on the system.

Complete step by step answer:
Before the collision,let the speed of bob $A$ be $v$ and the speed of bob $B$ is $u = 0$.After the collision the speed of bob $A$ becomes ${v_1}$ and speed of bob $B$ is ${v_2}$.According to law of conservation of momentum,
Initial moment of bob $A$ and $B$ before collision $=$final momentum after collision of bob $A$ and $B$
$mv + mu = m{v_1} + m{v_2}$
$\Rightarrow v = {v_1} + {v_2}$…(i)
For a perfectly elastic collision coefficient of Restitution is $e = 1$.
$e = \dfrac{{{v_2} - {v_1}}}{{v + u}} \\\ \Rightarrow e= \dfrac{{{v_2} - {v_1}}}{v}$
$\because e = 1$
$v = {v_1} - {v_2}$…(ii)
Solving (i) and (ii) we get,
$\therefore {v_1} = 0$

Therefore, bob $A$ will not rise since the speed becomes zero and the bob comes to rest.

Note: An elastic collision is a collision in which there is no loss in kinetic energy in the system as a result of collision. It is observed in an elastic collision that after the initial speeds of the two bodies get exchanged after collision. In the above situation also bob $B$ was at rest and bob $A$ was in motion but after collision bob $A$ comes to rest. In inelastic collision there is loss in energy which gets dissipated during the interaction.