Question

The bob of a pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. The bob will; then pass through its equilibrium position with a speed ν, where ν equals to :
A.$\sqrt[{}]{2gl(1-\sin \theta )}$
B.$\sqrt{2gl(1+\cos \theta )}$
C.$\sqrt{2gl(1-\cos \theta )}$
D.$\sqrt{2gl(1+\sin \theta )}$

Answer 1

Now at one of the extreme positions bob is held. So, at this point, it has gravitational potential energy and when it is released it gets converted to kinetic energy. So, by using the law of conservation of energy at mean position and bat extreme position we can find the requisite.

Complete step by step answer:
The length of the pendulum is l. Now when it is displaced from its equilibrium position and makes an angle-angle θ with the vertical, let h be the height above the equilibrium point. Now at one of the extreme positions Bob is held. So, at this point, it has gravitational potential energy and when it is released it gets converted to kinetic energy. So, by using the law of conservation of energy at mean position and bat extreme position we can find the requisite.

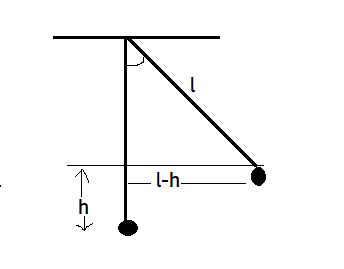
Energy at extreme position= energy at mean position
$mgh=\dfrac{m{{v}^{2}}}{2} \\\ \implies gh=\dfrac{{{v}^{2}}}{2} \\\ \therefore v=\sqrt{2gh} \\\$
Now,
$\cos \theta =\dfrac{l-h}{l} \\\ \implies l\cos \theta =l-h \\\ \implies h=l-l\cos \theta \\\ \therefore h=l(1-\cos \theta ) \\\$

So, the velocity becomes $v=\sqrt{2gl(1-\cos \theta )}$, this matches with option (C).

Note:
The pendulum has two extreme positions and one mean position. At the two extreme positions, the energy is potential and in between the two extreme positions the energy is potential plus kinetic and at the mean position, the energy is kinetic.