Question

The bob of a pendulum is released from a horizontal position. If the length of the pendulum is $1.5\ m$ , what is the speed with which the bob arrives at the lowermost point, given that it dissipated $5\%\$ of its initial energy against air resistance?

Answer 1

Hint: First of all we will consider the initial position of the bob and then the final position which is at the lowermost point. Then on applying the law of conservation of energy i.e. $\Delta E=K+P$ on two points we will find the velocity of the bob due to which it arrives at the lowermost point.

Formula used: $\Delta E=K+P$

Complete step by step answer:
In the question it is given that a bob of a pendulum is released from a horizontal position and length of the pendulum is $1.5\ m$ and we are asked to find the speed of the bob due to which it reaches the lowest most position. So, first of all we will draw the diagram for the simplicity in solving the problem,

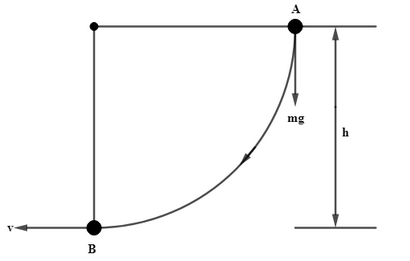
Now, we will consider the point A at height h from the ground, which is the initial position of the bob. At this position the pendulum is in a horizontal position.
Now, we know that in this position the kinetic energy of the bob will be zero as it is in the rest position but it will possess potential energy due to height of the bob from the ground, this can be given mathematically by using the law of conservation of energy as,
$\Delta E=K+P$ ………………..(i)
Where, K is Kinetic energy, P is Potential energy and E is total energy of the system,
Now, as kinetic energy is zero the total energy will be equal to potential energy at point A which can be given as,
$\Delta {{E}_{A}}=P$ …………..(ii)
Where, $P=mgh$.
Now, considering the point B, when bob will be released its potential energy will convert into kinetic energy and when the bob reaches lowermost position the height will be zero so the potential energy will be zero and it can be shown mathematically as,
$\Delta {{E}_{B}}=K$ ……………….(iii)
Where, $K=\dfrac{1}{2}m{{v}^{2}}$
Now, it is given that before reaching the lowermost position it loses $5\%\$of its initial energy, so it can be said that $95\%\$energy will be left which gets converted into kinetic energy. So, on applying law of conservation of energy for the system it can be said that energy at point A should be equal to energy at point B, which can be given mathematically as,
$\Delta {{E}_{A}}=\Delta {{E}_{B}}$
On substituting the values from expression (ii) and (iii) we will get,
${{K}_{A}}={{P}_{B}}$
$\Rightarrow \dfrac{1}{2}m{{v}^{2}}=\dfrac{95}{100}mgh$
Here, when the bob reaches the lower most position height will be equal to the length of the pendulum, it can shown mathematically as,
$l=h=1.5\ m$
Again, substituting these values we will get,
$\Rightarrow {{v}^{2}}=\dfrac{95}{100}\left( 10 \right)\left( 1.5 \right)\times 2$
$\Rightarrow v=\sqrt{28.5}=5.338\ m/s$
Hence, the speed of the bob while reaching the lower most point will be $5.338\ m/s$.

Note: Students might make mistakes in considering the law of conservation of energy at two points and they might not consider the potential energy as zero at the lowermost point and due to that they might not get the final answer to the problem. So, students must be careful while considering the law of conservation of energy.