Question
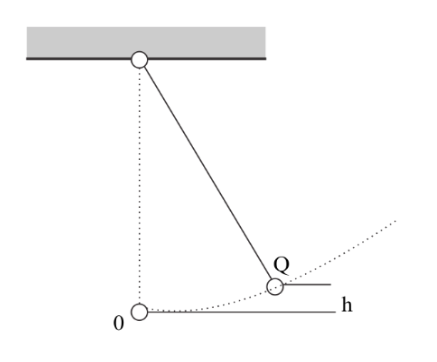
Question: The bob of a pendulum is displaced from its equilibrium position O to a position Q which is at heigh...
The bob of a pendulum is displaced from its equilibrium position O to a position Q which is at height ‘h’ above Q and the bob is then released. Assuming the mass of the bob to be ‘m’, and the time period to be 2 seconds, the tension in string when the bob passes through O is
A) m(g+2π2h)
B) m(g+π2h)
C) m(g+2π2h)
D) m(g+3π2h)
Solution
First of all, we will write the equation of tension at point O. We will then equate energies at both points i.e. O and Q. From there, we will calculate the values of unknown quantities and from the time period equation of the pendulum, we will find out the length of the pendulum. We will then put all these in the equation of tension and calculate its value.
Complete step-by-step solution:
The forces acting at point O will be- tension, weight of the pendulum. Let the length of the pendulum be l and v be its velocity at point O and τ be the tension in the string.
The mass of bob is m.
Equating the forces at O, we will get:
τ=lmv2+mg ……..(i)
Lets apply conservation of energy at point O and Q.
21mv2+mg(0)=21m(0)2+mgh ⇒21mv2=mgh ⇒21v2=gh ⇒v=2gh
We know that the time period of pendulum is given by-
T=2πgl ⇒2=2πgl ⇒(π1)2=gl ⇒l=π2g
Putting the values of velocity and length in equation (i), we get:
τ=π2gm(2gh)+mg ⇒τ=2mhπ2+mg ∴τ=m(g+2π2h)
Hence, the correct option is A.
Note- Tension is a kind of force which comes into play when two bodies pull each other(usually). While calculating tension here, we must keep in mind that not only weight of body but also an additional force will act on it too. Here, tension will not be equal to the weight of the body.
