Question
Question: The blocks have velocities as shown in the figure. Final velocity of the block C after all possible ...
The blocks have velocities as shown in the figure. Final velocity of the block C after all possible elastic collisions is
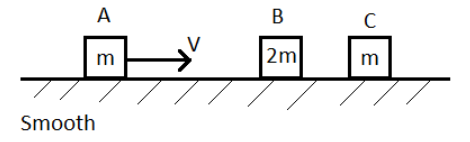
A) 98V
B) V
C) 94V
D) 2V
Solution
This problem can be solved by considering the problem as two subproblems – one involving the elastic collision between A and B and the other the elastic collision between B and C. Using the formulae for the final velocities of a body after an elastic collision, we can get the required final velocity of C after the collision with B.
Formula used:
v2=m1+m2m2−m1u2+m1+m22m1u1
Complete answer:
We will consider the two elastic collisions (between A and B and subsequently between B and C) separately and use the formula for the final velocity of a body in an elastic collision in terms of the masses of the two bodies and the initial velocities of the two bodies before the collision.
For an elastic collision between two bodies 1 and 2 of masses m1 and m2 respectively, the final velocity of body 2 is given by
v2=m1+m2m2−m1u2+m1+m22m1u1 --(1)
Where u2,u1 are the velocities of the bodies 1 and 2 just before the collision.
Now, for the collision between A and B –
The initial velocity of block A is uA=V.
The masses of A and B are mA=m and mB=2m respectively.
Since, the block B is at rest before the collision, its initial velocity is uB=0.
Let the final velocity of the block B after collision with A be vB.
Therefore, using (1), we get
vB=mB+mAmB−mA(uB)+mA+mB2mAuA
∴vB=2m+m2m−m0+m+2m2mV=0+3m2mV=32V --(2)
Now, the block B moves with a velocity 32V after collision with A and then goes on to hit C.
Therefore, for the collision of B with C –
The initial velocity of block B is the velocity of the block B after collision with A. It is =vB=32V.
The masses of B and C are mB=2m and mC=m respectively.
Since the block C is at rest before the collision, its initial velocity is uC=0.
Let the final velocity of the block C after collision with B be vC.
Therefore, using (1), we get
vC=mC+mBmC−mB(uC)+mB+mC2mBuB
∴vC=m+2mm−2m0+2m+m2(2m)32V=0+3m4m32V=98V
Hence, we have got the required final velocity of the block C as 98V.
Therefore, the correct option is A) 98V.
Note:
Students must note that in the equations for the final velocities of the bodies in the elastic collisions, that is, formula (1), the direction of motion of the bodies holds a lot of significance. For example, if two bodies are moving in the same direction before the collision, then they must be assigned velocities with the same sign (either both positive or both negative). However, if they were moving towards each other before the collision, then they must be assigned opposite signs of their speeds (one positive and the other negative).
