Question

The block of mass $m$ equal to $100kg$ is being pulled by a horizontal force $F = 2mg$ applied to a string as shown in figure (take $g = 10m/{s^2}$). The pulley is massless and is fixed at the edge of an immovable table. What is the value of force exerted by the supporting cable (rod) on the pulley ( in newton).

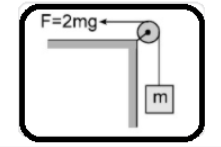
(A) $2mg$
(B) $\sqrt 2 mg$
(C) $2\sqrt 2 mg$
(D) $3\sqrt 2 mg$

Answer 1

Since the supporting rod is at rest we draw a free body diagram showing all the forces acting at the point of the supporting rod. The forces that are acting are the horizontal tension force, vertical tension force, and the force exerted by the support on the massless pulley. These forces are vectors ( direction based ) so we do vector addition. Adding all the three forces on the free body diagram we get zero as the system is at rest.

Complete step by step solution:
Taking ${T_1}, {T_2}, {F_S}$ As the tension force vertically, tension force horizontally, and force of support.

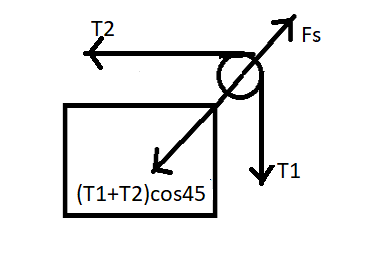
Adding all the three forces we get ,${{\vec T}_1} + {{\vec T}_2} + {{\vec F}_S} = 0$
The angle between the sum of the 2 tension forces and each tension force is $45^\circ$,
$\left| {{{\vec F}_S}} \right| = \left| {{{\vec T}_1} + {{\vec T}_2}} \right|$
${T_1} = {T_2}$
${F_S} = 4mg\cos (45^\circ )$
${F_s} = 2\sqrt 2 mg$
The unit of the force acting on the support is newton which is equal to mass times gravity.

Hence the answer is (C), $2\sqrt 2 mg$.

Additional information: Tension force is the force that is transmitted through a cable, rope, wire, or string when it is pulled tight by forces acting from opposite ends. It is directed along the length of the cable and pulls equally on the objects on the opposite ends of the wire. The tension on an object is equal to the product of the mass of the object and gravitational force added to the product of the mass and acceleration.

Note: We can also use vector addition instead if using $\cos (45°)$ which would lead us to the same answer. As,$\overrightarrow A + \overrightarrow B = \sqrt {{A^2} + {B^2} + 2ABCos\theta }$ as the angle between the two tension forces is 90° we still get the same answer at the end.