Question

The binding energies of two nuclei P and Q all and y joules. If 2x > y then the energy released in reaction

$P^n + P^n \rightarrow Q^{2n}$, will be

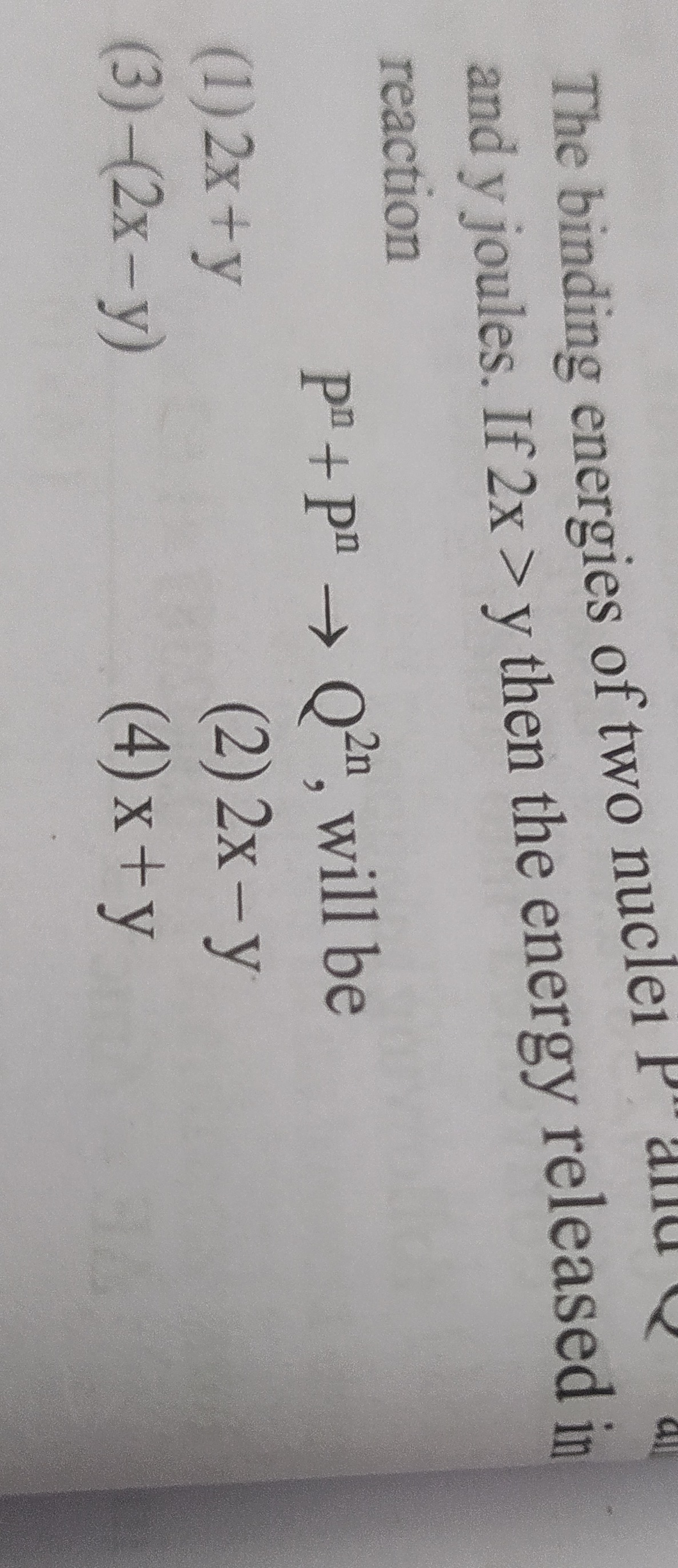
• A. 2x + y
• B. 2x - y
• C. -(2x - y)
• D. x + y

Answer 1

Answer: (B)

2x - y

Answer 2

The energy released in a nuclear reaction (Q-value) is given by the difference between the total binding energy of the products and the total binding energy of the reactants.

Given: Binding energy of nucleus P = x joules Binding energy of nucleus Q = y joules

The reaction is: $P^n + P^n \rightarrow Q^{2n}$

Total binding energy of reactants = Binding energy of P + Binding energy of P = x + x = 2x Total binding energy of products = Binding energy of Q = y

Energy released (Q) = (Total binding energy of products) - (Total binding energy of reactants) $Q = y - 2x$

The problem states that $2x > y$. This implies that $y - 2x$ will be a negative value.

However, in the context of multiple-choice questions asking for "energy released", if the calculated Q-value (BE_products - BE_reactants) is negative, it often implies that the question is asking for the magnitude of the energy change.

If the energy released is denoted by Q, and $Q = y - 2x$, then since $y - 2x < 0$, the reaction absorbs energy. The amount of energy absorbed is $-(y - 2x) = 2x - y$.

Thus, the answer would be $|y - 2x|$. Since $y - 2x$ is negative, $|y - 2x| = -(y - 2x) = 2x - y$.