Question

The biggest among $\left( {\sin 1 + \cos 1} \right),\left( {\sqrt {\sin 1} + \sqrt {\cos 1} } \right),\left( {\sin 1 - \cos 1} \right):$
A) $\left( {\sin 1 + \cos 1} \right)$
B) $\left( {\sqrt {\sin 1} + \sqrt {\cos 1} } \right)$
C) $\left( {\sin 1 - \cos 1} \right)$
D) None of these.

Answer 1

In trigonometric function, $\tan \theta$,
As angle approaches to zero ( $\theta \to 0$) , tangent of angle approached to infinity ($\tan \theta \to \infty$).
$\Rightarrow \tan 1$must be a larger value (atleast greater than 1); use this fact to find inequality between $\sin 1{\text{ }}\& {\text{ }}\cos 1$.
The Square of numbers for greater than 0 and less than 1, is smaller than the number.
For example: Square of 0.6
i.e. $\mathop {\left( {0.6} \right)}\nolimits^2 = 0.36$
0.36 < 0.6
The range is a set of all output values of function as independent variables varies thoughout the domain.
The domain is a set of all possible values on which function is defined.
For trigonometric function $y = \sin x$ , independent variable is x.
The domain is the set of all real numbers.
Range of trigonometric function $\sin x = \left[ { - 1,1} \right]{\text{ and }}\cos x = \left[ { - 1,1} \right]$

$$\Rightarrow \mathop {\left( {\sin x} \right)}\nolimits^2 < \sin x \\\ {\text{and }}\mathop {\left( {\cos x} \right)}\nolimits^2 < \cos x \\\$$

Use above mention property to find the inequality between $\sqrt {\sin 1} {\text{ }}\& {\text{ }}\sin 1$.

Complete step by step solution:
Step 1: Drawing a graph of the tangent function.

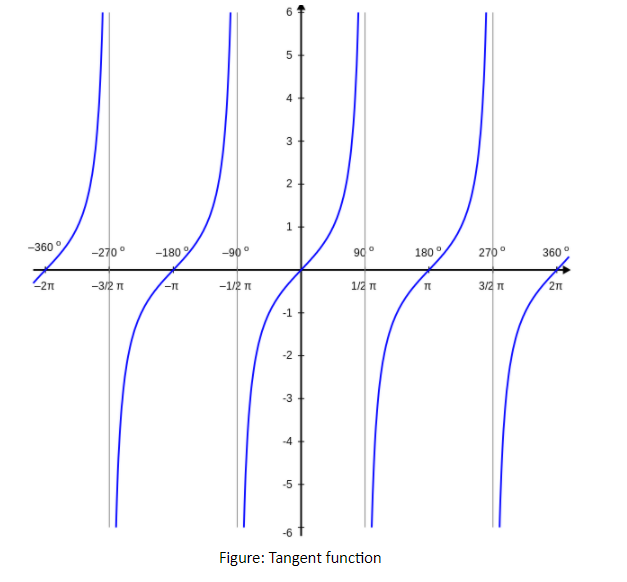
We know that $\tan 1 > 1$
It is known, $\tan 1 = \dfrac{{\sin 1}}{{\cos 1}}$
$\Rightarrow \dfrac{{\sin 1}}{{\cos 1}} > 1$
$\Rightarrow \sin 1 > \cos 1$ …… (1)
when smaller number is substracting form larger number, then result is real positive number.
$\Rightarrow \sin 1 - \cos 1 > 0$ (from (1))
Hence, $\sin 1$is positive (or greater than 0) and $\cos 1$is also positive (or greater than 0).
$\Rightarrow \sin 1 > 0;{\text{ cos1 > 0}}$
The Sum of two positive numbers is greater than their difference.
$\Rightarrow \left( {\sin 1 + \cos 1} \right) > \left( {\sin 1 - \cos 1} \right)$ …… (2)
Step 2: Draw graph of the sine function

Range of sine function: $\sin x = \left[ { - 1,1} \right]{\text{ }}$
$\Rightarrow \sin 1 < 1$
$\sqrt {\sin 1} > \sin 1$
Hence, for values less than ‘1’, higher power gives lower values
Example: For $\left( {0 < x < 1} \right)$
$x > \mathop x\nolimits^2 > \mathop x\nolimits^3 > \mathop x\nolimits^4 > \mathop x\nolimits^5 .....$
Similarly, $\sin 1 > {\sin ^2}1$
$\Rightarrow \sin 1 < \sqrt {\sin 1} \\\ \& \;{\text{ }}\cos 1 < \sqrt {\cos 1} \\\$
Thus, $\left( {\sqrt {\sin 1} - \sin 1} \right)$ and $\left( {\sqrt {\cos 1} - \cos 1} \right)$ are real positive number.
Then, $\left( {\sqrt {\sin 1} - \sin 1} \right) + \left( {\sqrt {\cos 1} - \cos 1} \right) > 0$
$\Rightarrow \left( {\sqrt {\sin 1} + \sqrt {\cos 1} - \sin 1 - \cos 1} \right) > 0$
On transferring number to the other side of the inequality, a sign of the number changes.
$\Rightarrow - \left( { + \sin 1 + \cos 1} \right) > - \left( {\sqrt {\sin 1} + \sqrt {\cos 1} } \right)$
Multiplying by a minus sign on both sides. The inequality reverses.
$\Rightarrow \left( {\sin 1 + \cos 1} \right) < \left( {\sqrt {\sin 1} + \sqrt {\cos 1} } \right)$ …… (3)
From (2) and (3)
$\left( {\sin 1 - \cos 1} \right) < \left( {\sin 1 + \cos 1} \right) < \left( {\sqrt {\sin 1} + \sqrt {\cos 1} } \right)$
Final answer: Among $\left( {\sin 1 + \cos 1} \right),\left( {\sqrt {\sin 1} + \sqrt {\cos 1} } \right),\left( {\sin 1 - \cos 1} \right)$; $\left( {\sqrt {\sin 1} + \sqrt {\cos 1} } \right)$is the biggest.

$\therefore$ The correct option is (B).

Note:
The range of a function is defined as the set of all values of the function defined on its domain.
Range and domain of some trigonometric functions are given below:

Trigonometric function	Domain	Range
Sine	$\left( { - \infty , + \infty } \right)$	[-1,1]
Cosine	$\left( { - \infty , + \infty } \right)$	[-1,1]
Tangent	All real numbers except $\dfrac{\pi }{2} + n\pi$	$\left( { - \infty , + \infty } \right)$
Cosecant	All real numbers except $n\pi$	$\left( { - \infty , - 1} \right] \cup \left[ {1, + \infty } \right)$
Secant	All real numbers except $\dfrac{\pi }{2} + n\pi$	$\left( { - \infty , - 1} \right] \cup \left[ {1, + \infty } \right)$
Cotangent	All real numbers except $n\pi$	$\left( { - \infty , + \infty } \right)$