Question

The benches of a gallery in a cricket stadium are 1m wide and 1m high. A batsman strikes the ball at a level 1m above the ground and hits a mammoth sixer. The ball starts at 35 m/s at an angle of 530 with horizontal. The benches are perpendicular to the plane of motion and the first bench is 110 m from the batsman. On which bench will the ball hit?

Answer 1

Hint: The ball moves with a velocity at an angle to the horizontal. So, the ball will follow a projectile motion. Define the projectile motion obtain the mathematical expression for the equation of motion for an object in projectile motion.

Complete Step by Step answer:

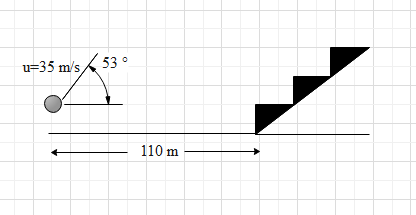
Let us consider the whole field in a coordinate system. The horizontal side is represented by y-axis and the vertical side is represented by the x-axis with the batsman at position $x=0,y=0$

The ball is hit at x =0 y =1 m.
The benches in the gallery are 1 m wide and 1 m high. They form a slope in the gallery.

Slope of stair case of benches in gallery is given by

=$\dfrac{\text{height of step}}{\text{width of step}}=\dfrac{1m}{1m}=1$

The line joining the feet of the benches i.e. the line along slope of the benches will be = $\dfrac{y-1}{x-110}=1$
Where the bottom point of the bench is (110,1) and 1 is the slope of the line along the benches.
Solving the above equation, we get,

$y=x-109\text{ }\to \text{1}$

Equation of trajectory of cricket ball in projectile motion is:

$x=ut\cos \theta$
$t=\dfrac{x}{u\cos \theta }$

& y=ut\sin \theta -\dfrac{1}{2}g{{t}^{2}} \\\ & \text{By, putting the value of t, we get} \\\ & y=x\tan \theta -g\dfrac{g{{x}^{2}}}{2{{u}^{2}}{{\cos }^{2}}\theta } \\\ & y=1.327x-\dfrac{9.8{{x}^{2}}}{2\times {{(35)}^{2}}\times 0.362} \\\ & y=1.327x-0.011{{x}^{2}}\text{ }\to \text{ 2} \\\ \end{aligned}$$ Substitute y from equation 1 $$\begin{aligned} & x-109=1.327x-0.011{{x}^{2}} \\\ & 0.011{{x}^{2}}-0.327x-109=0 \\\ & x=\dfrac{(0.327+2.21)}{2\times 0.011} \\\ & x=115.32m \\\ \end{aligned}$$ y at 115.32m is =$$115.32-109=6.32$$ y = 6.32 m So, it is the 6th bench, as the $1st$ bench is from 110m to 111m, 6th bench is from 115 m to 116m. Note: If instead of the gallery we have an empty field and we need to find the distance the ball will travel, then we can directly use the mathematical expression for maximum range. In this question, we need to find the point at which the trajectory of the ball intersects with the line joining the feet of the benches.