Question
Question: The battery in the diagram is to be charged by the generator G. The generator has a terminal voltage...
The battery in the diagram is to be charged by the generator G. The generator has a terminal voltage of 120 volts when the charging current is 10 amperes. The battery has an emf of 100 volts and internal resistance of 1 ohm. In order to charge the battery at 10 amperes charging current, the resistance R should be set at:
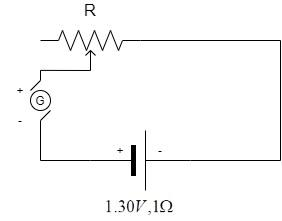
Solution
There are two kinds of battery: Primary and Secondary. Primary battery is a single use battery which cannot be recharged for reusing again. Secondary battery is a reusable battery which can be charged and discharged. Examples of such battery are – Primary – Dry Leclanche cell made of zinc-carbon, Zinc manganese dioxide cell Secondary – Lead acid, Nickel-Cadmium
Complete step-by-step answer:
The emf is defined as the total voltage that is available for the discharge in the circuit. However, due to internal resistance, not all the emf is completely used. Therefore, some of the emf gets wasted in overcoming the internal resistance, and what remains flows in the circuit, which is termed as the terminal voltage.
For example, if 12 V is the emf of the cell, not all 12V is the potential difference in the circuit. The terminal voltage can be equal to 9V or 10V.
Here, given:
Terminal voltage of generator, V=120V
Charging current, I=10A
Internal resistance, r=1Ω
By the definition of terminal voltage, we have –
V=E−Ir where E is the emf.
By substituting the above values, we can calculate the emf of the generator –
E=V+Ir E=120+10(1) →E=130V
In the circuit, the net resistance of the circuit,
R=IE−V
Substituting the values, we get –
R=IE−V R=10130−120 →R=1010=1Ω
Therefore, the resistance R must be set to 1Ω.
Note: The students must keep in mind that the terminal voltage value is always lesser than the emf. So, if you ever get the value of emf lesser than the terminal voltage, stop right there and trace back the steps because there is a 100% chance that you are doing the problem wrong. This can help you avoid computational errors in your competitive exams.
