Question

The balloon, the light rope and the monkey shown in the below figure at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend?

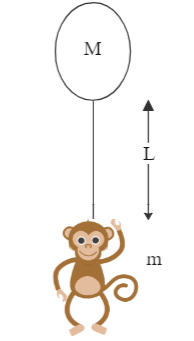
Consider the mass of the balloon as $M$ , mass of the monkey as $m$ , and the length of the rope ascended by the monkey as $L$

Answer 1

Hint
In a system of bodies involving masses, the centre of mass is the point where the forces can be assumed to be acting as if applied on the whole body. As the position of masses in the system changes, the centre of mass also shifts.
Formula used: ${x_{cm}} = \dfrac{{{x_1}{m_1} + {x_2}{m_2}}}{{{m_1} + {m_2}}}$ , where ${m_1}$ and ${m_2}$ are masses in a two-body system, ${x_1}$ and ${x_2}$ are their respective positions, and ${x_{cm}}$ is the position of the centre of mass.

Complete step by step answer
In this problem, we have a two-body system consisting of the monkey and the balloon. They are initially at rest in the air, but then the monkey moves some distance upwards. This wall causes the balloon to travel some distance as well, to keep the centre of mass intact.
In this problem we need to find the new centre of mass position, and this would be the amount by which the balloon would descend to keep the balance.
We know that the centre of mass can be calculated as:
$\Rightarrow {x_{cm}} = \dfrac{{{x_1}{m_1} + {x_2}{m_2}}}{{{m_1} + {m_2}}}$
We are provided with the following data:
Mass of the monkey is $m$ . This will be our ${m_1}$
Mass of the balloon is $M$ . This will be our ${m_2}$
Distance the monkey covers is $L$
Hence, ${x_1}$ for the monkey will be $L$ as this is the distance by which it ascends, and similarly, ${x_2}$ for the balloon will be zero as it does not move.
Putting the values gives us the new position as:
$\Rightarrow x = \dfrac{{m \times L + M \times 0}}{{m + L}}$ [Since the balloon does not travel any distance initially]
Upon solving, we get:
$\Rightarrow x = \dfrac{{mL}}{{m + L}}$
Hence, the distance descended by the balloon is $\dfrac{{mL}}{{m + L}}$ .

Note
To understand this concept better, let us take an example. Suppose you are balancing an eraser and a sharpener on a ruler. As these two have different masses, their positions will need to be constantly adjusted to reach a point where the scale is balanced. If you move the eraser by some distance, naturally the balance would be gone and the scale would start to wobble. Only when you shift the sharpener by some distance, the scale would be balanced again. This happens because the position of the centre of mass changed the second time, and this is the amount by which the sharpener needs to be shifted too.