Question

The ballistic pendulum is an apparatus used to measure the speed of a fast moving projectile, such as a bullet. A bullet of mass m is fired into a large block of wood of mass $M$ suspended from light wires. The bullet embeds in the block and the entire system swings to a height $h$. What is the initial speed of the bullet in terms of height $h$?

& A.\dfrac{m}{M}\sqrt{2gh} \\\ & B.\dfrac{m}{M+m}\sqrt{2gh} \\\ & C.\dfrac{M+m}{m}\sqrt{2gh} \\\ & D.\sqrt{\dfrac{2m}{M+m}2gh} \\\ \end{aligned}$$

Answer 1

An elastic collision occurs when the total momentum and the energy of the two bodies interacting bodies is conserved. Here, we can consider the interaction of the molecules with each other to be in one direction and solve the following.

Formula used: $P=mv$, $K.E=\dfrac{1}{2}mu$ and $P.E=mgh$

Complete step by step answer:
We know that collision is the interaction between two bodies which are moving with some velocities for a short duration of time. We also know that when two bodies undergo collision there is a transfer of momentum and energy between the bodies. Generally, collision results in the change in velocity of the interacting bodies. Since velocity is a vector, we can say that collision changes the direction and speed of the interacting bodies.
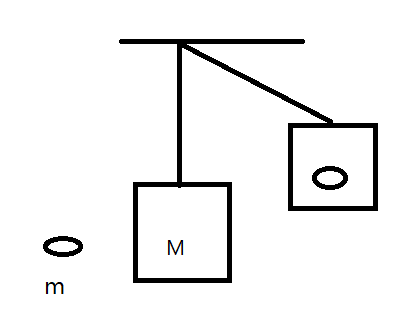
Let us consider that the mass of the bullet is m moves with an initial velocity $u$ . Let the mass of the block be $M$ be at rest initially. When the bullet hits the block, let both the block and the bullet rise to a height $h$ with a final velocity $v$, as shown in the figure below.
If the collision of the block and the mass is considered to be elastic, then the momentum and the energy of the system is conserved.
$mu=(m+M)v$
$\implies v=\dfrac{mu}{m+M}$

We also know that, the kinetic energy is the energy possessed by the objects in motion. While potential energy is the energy due to height. Also, since the kinetic energy of the system is transferred as potential energy, we have
$\dfrac{1}{2}(m+M)v^{2}=(m+M)gh$
$\implies v^{2}=2gh$
$\implies \dfrac{mu}{m+M}=\sqrt{2gh}$
$\implies u=\dfrac{m+M}{m}\sqrt{2gh}$

So, the correct answer is “Option C”.

Note: Collision can be broadly classified into two types of collision namely the elastic collision, and the inelastic collision. In elastic collision, both the momentum and the kinetic energy of the system is conserved. In inelastic collisions, the momentum of the system is conserved while the kinetic energy is not conserved. Here, for simplicity, we are assuming that the above collision is elastic.