Question

The average P.E. of a body executing S.H.M. is :

$$\left( 1 \right)\dfrac{1}{2}k{A^2} \\\ \left( 2 \right)\dfrac{1}{4}k{A^2} \\\ \left( 3 \right)3k{A^2} \\\ \left( 4 \right)zero \\\$$

Answer 1

Law of conservation of energy states that the total of all forms of energies possessed by a moving object is always constant.
During any process energy can neither be created nor be destroyed it can be only converted from one form to another
In SHM the potential energy of the system is continuously converting from potential energy to kinetic energy and the again to potential energy

Complete step by step solution:
Simple harmonic motion:
repetitive movement back and forth through an equilibrium, or central, position, so that the maximum displacement on one side of this position is equal to the maximum displacement on the other side.
In SHM the potential energy of any object is maximum at the two far ends and the kinetic energy is maximum at the midpoint
Refer figure:

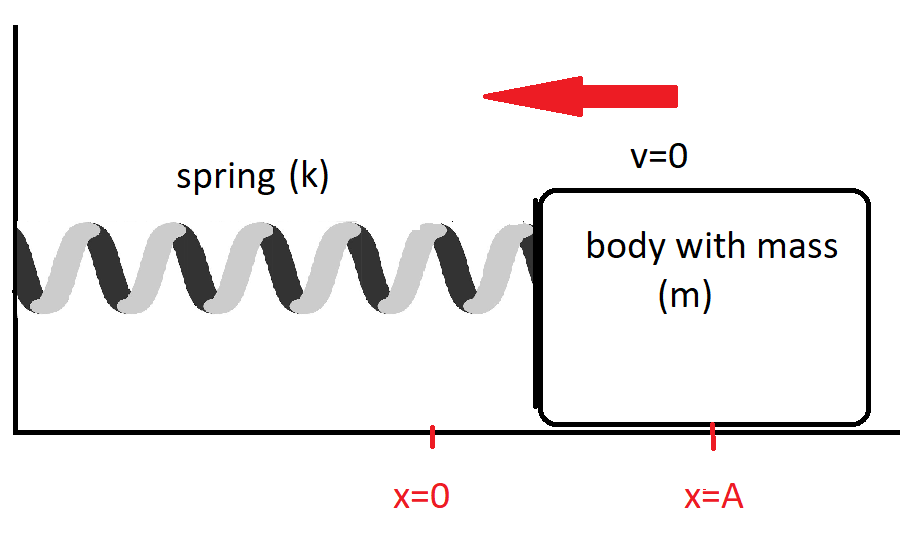
Now as we know that the motion of the block on a spring in SHM is defined by the position $x\left( t \right) = A\cos \left( {\omega t + \phi } \right)$$\left( 1 \right)$
We know that derivating position to time we get velocity,
So $v(t) = - A\omega {\text{sin}}(\omega t + \phi )$____________$\left( 2 \right)$
As per the law of conservation of energy
Total energy = Kinetic energy $+$Potential energy
$\Rightarrow {E_{total}} = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}k{x^2}$
Where
$m$: the mass of the block
k: spring constant
v: velocity of the object
x: displacement
${E_{total}} = \dfrac{1}{2}m{A^2}{\omega ^2}{\sin ^2}\left( {\omega t + \phi } \right) + \dfrac{1}{2}k{A^2}{\cos ^2}\left( {\omega t + \phi } \right)$
As $\omega = \sqrt {\dfrac{k}{m}}$

$$\therefore {E_{total}} = \dfrac{1}{2}m{A^2}\left( {\dfrac{k}{m}} \right){\sin ^2}\left( {\omega t + \phi } \right) + \dfrac{1}{2}k{A^2}{\cos ^2}\left( {\omega t + \phi } \right) \\\ \Rightarrow {E_{total}} = \dfrac{1}{2}k{A^2}{\sin ^2}\left( {\omega t + \phi } \right) + \dfrac{1}{2}k{A^2}{\cos ^2}\left( {\omega t + \phi } \right) \\\ \Rightarrow {E_{total}} = \dfrac{1}{2}k{A^2}\left[ {{{\sin }^2}\left( {\omega t + \phi } \right) + {{\cos }^2}\left( {\omega t + \phi } \right)} \right] \\\ \\\$$

Again as ${\sin ^2}\theta + {\cos ^2}\theta = 1$
We get ${E_{total}} = \dfrac{1}{2}k{A^2}$______________________________(3)

Now to find average potential energy we know that in SHM as K.E increases P.E decreases and vice versa but total energy at all the points remains the same as the sum of K.E and P.E. from here we can conclude that average potential energy will be half of the total energy.
Refer figure:

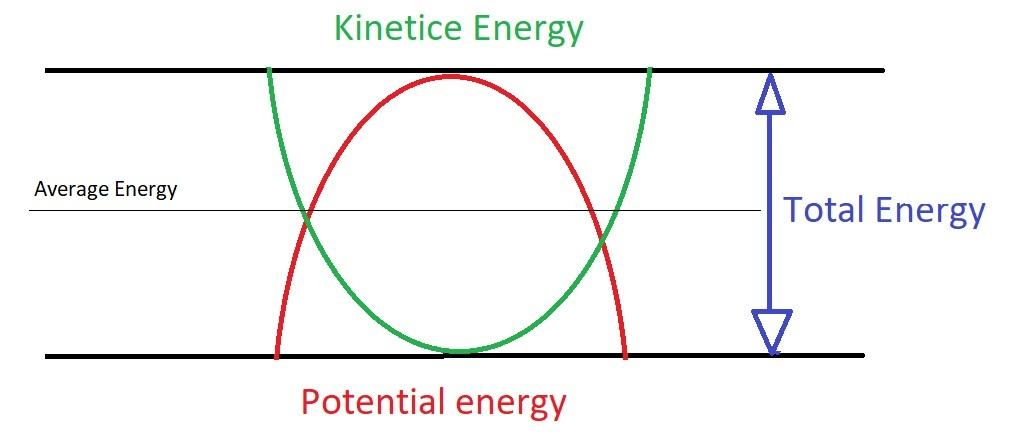
So,

$${\left( {P.E} \right)_{avg}} = \dfrac{{{E_{total}}}}{2} \\\ \therefore {\left( {P.E} \right)_{avg}} = \dfrac{{\dfrac{1}{2}k{A^2}}}{2} \\\ \Rightarrow {\left( {P.E} \right)_{avg}} = \dfrac{{k{A^2}}}{4} \\\$$

(2) The average potential energy of an object in SHM will be ${\left( {P.E} \right)_{avg}} = \dfrac{{k{A^2}}}{4}$

Note:

1. Energy is always conserved i.e.; the sum of all energies remains constant
2. As the object moves from an extreme position to the centre it's kinetic energy will increase from zero to maximum and then as it again moves from centre to another end it will decrease from a maximum at the centre to zero at ends.
3. The potential energy of the object is maximum at the end to zero at the centre
4. At every point in SHM, the total of kinetic energy and potential energy remains constant throughout.