Question

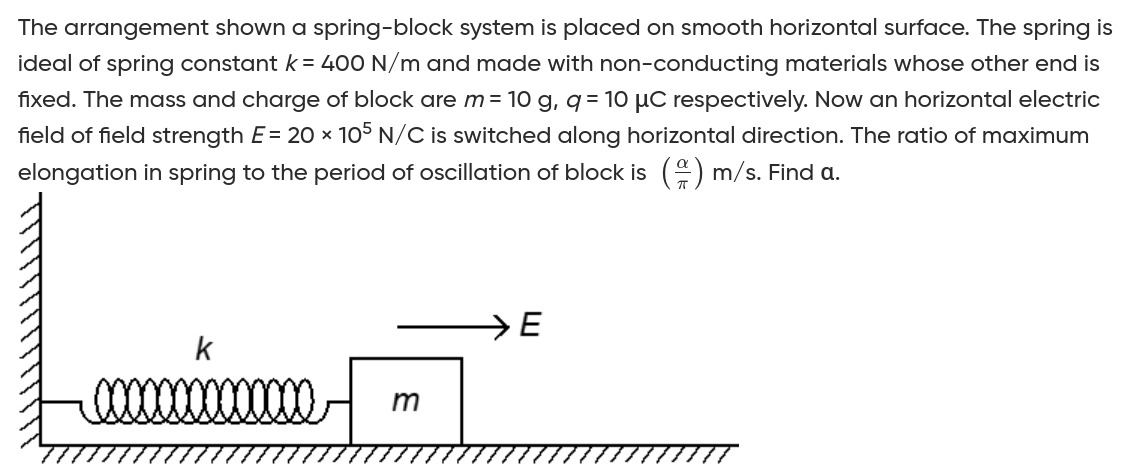
The arrangement shown a spring-block system is placed on smooth horizontal surface. The spring is ideal of spring constant $k = 400$ N/m and made with non-conducting materials whose other end is fixed. The mass and charge of block are $m = 10$ g, $q = 10 \mu$C respectively. Now an horizontal electric field of field strength $E = 20 \times 10^5$ N/C is switched along horizontal direction. The ratio of maximum elongation in spring to the period of oscillation of block is $(\frac{\alpha}{\pi})$ m/s. Find $\alpha$.

Answer 1

10

Answer 2

The problem describes a spring-block system on a smooth horizontal surface. An electric field is switched on, causing the charged block to oscillate. We need to find the ratio of the maximum elongation in the spring to the period of oscillation and then determine the value of $\alpha$.

1. Identify Given Parameters:

• Spring constant, $k = 400$ N/m
• Mass of the block, $m = 10$ g $= 10 \times 10^{-3}$ kg $= 0.01$ kg
• Charge of the block, $q = 10 \mu$C $= 10 \times 10^{-6}$ C $= 10^{-5}$ C
• Electric field strength, $E = 20 \times 10^5$ N/C

2. Calculate Maximum Elongation ($x_{max}$):

Initially, the spring is unstretched, and the block is at rest. When the electric field is switched on, the block experiences a constant electric force $F_e = qE$ in the direction of the field. This force acts as a constant external force on the spring-mass system.

The system will oscillate about a new equilibrium position where the net force is zero. Let the equilibrium elongation be $x_{eq}$. At equilibrium: $qE - kx_{eq} = 0$ So, $x_{eq} = \frac{qE}{k}$.

Since the block is released from rest at the initial unstretched position ($x=0$), this position is one extreme of the oscillation. The equilibrium position $x_{eq}$ is the center of oscillation. The amplitude of oscillation ($A$) is the distance from the equilibrium position to an extreme position. Therefore, $A = x_{eq} - 0 = x_{eq} = \frac{qE}{k}$.

The maximum elongation ($x_{max}$) occurs at the other extreme of the oscillation, which is $x_{eq} + A$. $x_{max} = x_{eq} + A = \frac{qE}{k} + \frac{qE}{k} = \frac{2qE}{k}$.

Alternatively, using the work-energy theorem: The initial kinetic energy is $KE_i = 0$. The initial spring potential energy is $U_{s,i} = 0$. At maximum elongation $x_{max}$, the block momentarily comes to rest, so $KE_f = 0$. The final spring potential energy is $U_{s,f} = \frac{1}{2}kx_{max}^2$. The work done by the electric field is $W_e = F_e \times x_{max} = qE x_{max}$. By the work-energy theorem, $W_{net} = \Delta KE$. Here, $W_{net} = W_e - W_s$, where $W_s$ is work done by spring force. Or, considering electric potential energy, the total mechanical energy (including spring potential and electric potential) is conserved if we define electric potential energy as $-qEx$. Let's use the work-energy principle: Work done by non-conservative forces (here, we treat electric force as doing work, and spring force is conservative and its work is included in potential energy change). $W_e = \Delta U_s + \Delta KE$ $qE x_{max} = (\frac{1}{2}kx_{max}^2 - 0) + (0 - 0)$ $qE x_{max} = \frac{1}{2}kx_{max}^2$ Since $x_{max} \neq 0$, we can divide by $x_{max}$: $qE = \frac{1}{2}kx_{max}$ $x_{max} = \frac{2qE}{k}$

Now, substitute the given values: $x_{max} = \frac{2 \times (10^{-5} \text{ C}) \times (20 \times 10^5 \text{ N/C})}{400 \text{ N/m}}$ $x_{max} = \frac{2 \times 20}{400}$ m $x_{max} = \frac{40}{400}$ m $x_{max} = \frac{1}{10}$ m $= 0.1$ m

3. Calculate Period of Oscillation ($T$):

The period of oscillation of a spring-mass system is given by the formula: $T = 2\pi\sqrt{\frac{m}{k}}$ Substitute the given values: $T = 2\pi\sqrt{\frac{0.01 \text{ kg}}{400 \text{ N/m}}}$ $T = 2\pi\sqrt{\frac{1}{40000}}$ s $T = 2\pi \frac{1}{\sqrt{4 \times 10^4}}$ s $T = 2\pi \frac{1}{2 \times 10^2}$ s $T = 2\pi \frac{1}{200}$ s $T = \frac{\pi}{100}$ s

4. Calculate the Ratio:

The ratio of maximum elongation in spring to the period of oscillation is $\frac{x_{max}}{T}$. Ratio $= \frac{0.1 \text{ m}}{\frac{\pi}{100} \text{ s}}$ Ratio $= \frac{0.1 \times 100}{\pi}$ m/s Ratio $= \frac{10}{\pi}$ m/s

5. Find $\alpha$:

The problem states that the ratio is $(\frac{\alpha}{\pi})$ m/s. Comparing our calculated ratio with the given form: $\frac{\alpha}{\pi} = \frac{10}{\pi}$ Therefore, $\alpha = 10$.