Question

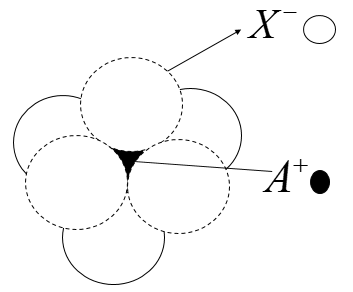
The arrangement of ${X^ - }$ ions around ${A^ - }$ ion in solid A X is given within the figure (not drawn to scale). If the radius of ${X^ - }$ is 250 pm, the radius of ${A^ + }$ is

A.$104pm$
B.$125pm$
C.$183pm$
D.$57pm$

Answer 1

We have to remember that the number of atoms or ions which will surround the central atom during a crystal lattice is understood because of the coordination number of the atom or ion. The coordination number of the cation in the crystal structure depends on the limiting radius ratio.

Complete step by step answer:
Given data contains:
The radius of ${X^ - }$ is 250 pm
Now we find the radius of A- as,
We must remember that the ratio of the ionic radii of the positive ion to the negative ion is understood as the limiting radius ratio.
According to the given figure, ${A^ + }$ is present in the octahedral void of ${X^ - }$ . The limiting radius in an octahedral void is said to be the radius of the sphere.
${r_{void}} = 0.414 \times {r_{sphere}}$
${r_{{A^ + }}} = 0.414 \times {r_{{X^ - }}}$
On substituting the given values we get,
${r_{{A^ + }}} = 0.414 \times 250$
On simplification we get,
${r_{{A^ + }}} = 103.5 \cong 104pm$
Therefore, the solution to this present question is option A that is 104pm.

Note:
Now we can discuss the significance of the limiting radius ratio follows as,
-The limiting X- radius ratio helps in predicting the structures of the ionic solids.
-The structure of an ionic compound mainly depends on the dimension of its constituent ions and therefore the stoichiometry. In the crystal lattice, the cations are surrounded by the largest number of possible anions. As the limiting radius ratio increases, the coordination number increases. But because the anions have an equivalent charge they repel and therefore the structure becomes unstable. As the radius ratio increases the size of the cation also increases. As a result the coordination number of the cation increases.