Question

The areas of two similar triangles are $36c{m^2}$ and $100c{m^2}$. If the length of a side of the smaller triangle is 3 cm, find the corresponding side of the larger triangle.

Answer 1

Hint: If two triangles are similar, then the ratio of the area of both triangles is proportional to the square of the ratio of their corresponding sides.

Complete step-by-step answer:

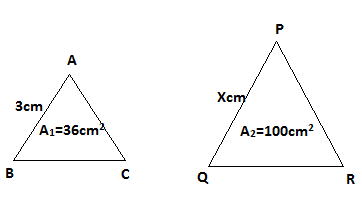
Area of smaller triangle ABC ${A_1} = 36c{m^2}$ .
Area of larger triangle PQR ${A_2} = 100c{m^2}$ .
Length of a side of the smaller triangle $AB = 3cm$
Let Length of the corresponding side of the larger triangle $PQ = x$ cm.
We know two triangles are similar So, the ratio of the area of both triangles is proportional to the square of the ratio of their corresponding sides.
$\frac{{area\left( {\vartriangle ABC} \right)}}{{area\left( {\vartriangle PQR} \right)}} = {\left( {\frac{{AB}}{{PQ}}} \right)^2} = {\left( {\frac{{AC}}{{PR}}} \right)^2} = {\left( {\frac{{BC}}{{QR}}} \right)^2}...............\left( 1 \right)$
We know the value of the value of $\vartriangle ABC = {A_1} = 36c{m^2},\vartriangle PQR = {A_2} = 100c{m^2},AB = 3cm$ So, we take first two fraction from (1) equation.
$\Rightarrow \frac{{area\left( {\vartriangle ABC} \right)}}{{area\left( {\vartriangle PQR} \right)}} = {\left( {\frac{{AB}}{{PQ}}} \right)^2} \\\ \Rightarrow \frac{{{A_1}}}{{{A_2}}} = {\left( {\frac{3}{x}} \right)^2} \\\ \Rightarrow \frac{{36}}{{100}} = {\left( {\frac{3}{x}} \right)^2} \\\ \Rightarrow {\left( {\frac{6}{{10}}} \right)^2} = {\left( {\frac{3}{x}} \right)^2} \\\$
Take the square root on both sides.
$\Rightarrow \frac{6}{{10}} = \frac{3}{x}$
Cross multiply
$\Rightarrow 6x = 30 \\\ \Rightarrow x = 5cm \\\$
So, the Length of the corresponding side of the larger triangle is 5cm.

Note: Whenever we face such types of problems we use some important points. First draw the figure of both triangles and mark the values of areas and corresponding sides then use the property of areas of similar triangles. So, we can easily get the required answer.