Question

The area of triangle with vertices (1, 2, 0), (1, 0, a) and (0, 3, 1) is $\sqrt{6}$ sq. units, then the values of a are

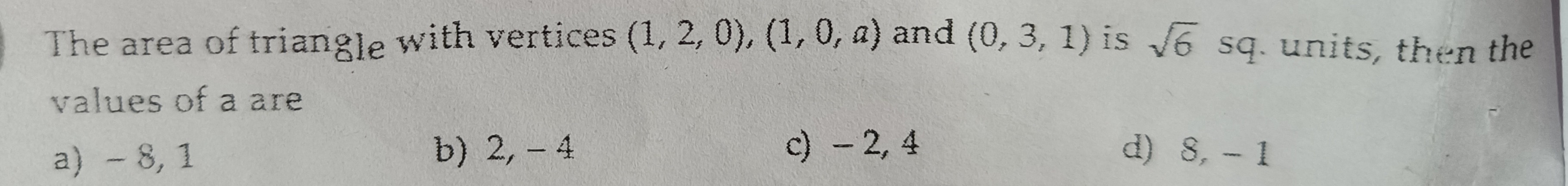
• A.
  • 8, 1
• B. 2, -4
• C. -2, 4
• D. 8, -1

Answer 1

Answer: (B)

2, -4

Answer 2

Solution:

Let the vertices be:

$A = (1, 2, 0)$, $B = (1, 0, a)$, $C = (0, 3, 1)$.

1. Find vectors:

$AB = B - A = (0, -2, a)$

$AC = C - A = (-1, 1, 1)$

2. Compute the cross product:

$AB \times AC = ( (-2 \cdot 1 - a \cdot 1), -(0 \cdot 1 - a \cdot (-1)), 0 \cdot 1 - (-2)(-1) )$ $= ( -2 - a, -a, -2 )$

3. Its magnitude is:

$|AB \times AC| = \sqrt{[(a + 2)^2 + a^2 + 2^2]} = \sqrt{[(a + 2)^2 + a^2 + 4]}$ $= \sqrt{[a^2 + 4a + 4 + a^2 + 4]} = \sqrt{[2a^2 + 4a + 8]}$

4. The area of the triangle is $\frac{1}{2}|AB \times AC|$. Given that area = $\sqrt{6}$, set:

$\frac{1}{2}\sqrt{(2a^2 + 4a + 8)} = \sqrt{6}$

$\Rightarrow \sqrt{(2a^2 + 4a + 8)} = 2\sqrt{6}$

Square both sides: $2a^2 + 4a + 8 = 4 \times 6 = 24$

$\Rightarrow 2a^2 + 4a - 16 = 0$

Divide by 2: $a^2 + 2a - 8 = 0$

5. Solve the quadratic:

$a^2 + 2a - 8 = 0$

$(a+4)(a-2) = 0$

Thus, $a = 2$ or $a = -4$

Explanation (Minimal):

• Compute AB and AC.
• Find $AB \times AC = (-(a+2), -a, -2)$.
• Set $\frac{1}{2}\sqrt{[(a+2)^2 + a^2 + 4]} = \sqrt{6}$, square to get $a^2 + 2a - 8 = 0$.
• Solve to get $a = 2$ or $a = -4$.