Solveeit Logo
Login

Question

Question: The area of triangle formed by the tangents from point (3,2) to hyperbola \({{x}^{2}}-9{{y}^{2}}=9\)...

The area of triangle formed by the tangents from point (3,2) to hyperbola x2−9y2=9{{x}^{2}}-9{{y}^{2}}=9 and the chord of contact w.r.t. point (3,2) is :

Explanation

Solution

Hint: Start by finding the equation of the chord of contact followed by the points where the chord of contact meets the hyperbola. Now once you know the points, you know all the three vertices of the triangle, so use the formula of area of the triangle with given vertices to get the answer.

Complete step by step solution:
First let us write the equation of hyperbola in standard form. On doing so, we get
x2−9y2=9{{x}^{2}}-9{{y}^{2}}=9
⇒x29−y2=1\Rightarrow \dfrac{{{x}^{2}}}{9}-{{y}^{2}}=1
Let us start by drawing a representative diagram of the situation given in the figure.

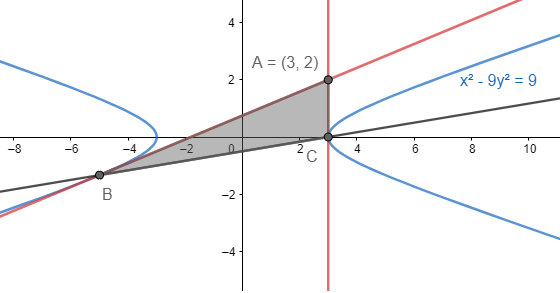
Now we know that one of the vertices of the triangle is (3,2). We also know that the chord of contact to the hyperbola x2a2−y2b2=1\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 w.r.t. point (p,q) is given by pxa2−qyb2=1\dfrac{px}{{{a}^{2}}}-\dfrac{qy}{{{b}^{2}}}=1 . So, the chord of contact given in the question is:
3x9−2y=1\dfrac{3x}{9}-2y=1
⇒x=3(2y+1)............(i)\Rightarrow x=3\left( 2y+1 \right)............(i)
Now, if we solve the equation of chord of contact with the equation of hyperbola, the points we get are the other two vertices of the triangle. So, substituting x from equation (i) in equation of hyperbola, we get
9(2y+1)29−y2=1\dfrac{9{{\left( 2y+1 \right)}^{2}}}{9}-{{y}^{2}}=1
We know that (a+b)2=a2+b2+2ab{{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab .
4y2+1+4y−y2=14{{y}^{2}}+1+4y-{{y}^{2}}=1
⇒3y2+4y=0\Rightarrow 3{{y}^{2}}+4y=0
⇒y(3y+4)=0\Rightarrow y\left( 3y+4 \right)=0
So, the possible values of y are 0 and −43-\dfrac{4}{3} .
If we put y=0 in equation (i), we get x=3. Also, if we put y to be −43-\dfrac{4}{3} , we get x=-5.
So, the vertices of the triangle are (3,2), (3,0) and (−5,−43)\left( -5,-\dfrac{4}{3} \right) .
Now we know that the area of the triangle is equal to the absolute value of:
12∣1x1y1 1x2y2 1x3y3 ∣=12∣132 130 1−5−43 ∣=12(1(−4−0)−1(−4+10)+1(0−6))=−8\dfrac{1}{2}\left| \begin{matrix} 1 & {{x}_{1}} & {{y}_{1}} \\\ 1 & {{x}_{2}} & {{y}_{2}} \\\ 1 & {{x}_{3}} & {{y}_{3}} \\\ \end{matrix} \right|=\dfrac{1}{2}\left| \begin{matrix} 1 & 3 & 2 \\\ 1 & 3 & 0 \\\ 1 & -5 & \dfrac{-4}{3} \\\ \end{matrix} \right|=\dfrac{1}{2}\left( 1\left( -4-0 \right)-1\left( -4+10 \right)+1\left( 0-6 \right) \right)=-8
So, the answer to the above question is 8sq units. Area is not to be negative and write it as |-8|.

Note: You could have also solved the questions by finding the tangents and the chord of contact, but that would be lengthy and complex to solve. Also, you need to learn all the formulas related to standard conic sections as they are used very often.