Question

The area of the upper face of a rectangular block is $0.5m\times 0.5m$ and the lower face is fixed. The height of the block is 1cm. A shearing force applied to the top face produces a displacement of 0.015mm. Find the strain and shearing force. (Modulus of rigidity,$\eta =4.5\times {{10}^{10}}N{{m}^{-2}}$)

Answer 1

Firstly you could recall the definition for shearing strain and hence its expression. Now we are readily given the values to be substituted and thus substituting them we get the value of shearing strain. Similarly, we could recall the expression for modulus of rigidity and then rearrange to get the shearing force. Now substitute the given values to get the shearing force.

Formula used:
Shearing strain,
$\theta =\dfrac{\Delta x}{h}$
Shearing force,
$F=\eta A\theta$

Complete step by step solution:
In the question, we are given the area (A) of the upper face of the rectangular block as,
$A=0.5m\times 0.5m=0.25{{m}^{2}}$
The height (h) of the block is given as,
$h=1cm={{10}^{-2}}m$
On application of shearing force on the top face of the block, it results in a displacement (x) given by,
$\Delta x=0.015mm=0.015\times {{10}^{-3}}m$
We are also given the modulus of rigidity as,
$\eta =4.5\times {{10}^{10}}N{{m}^{-2}}$

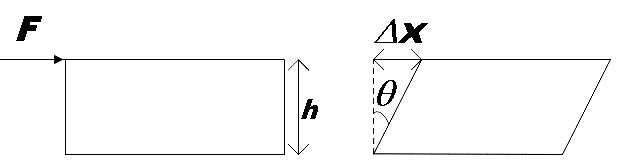
We know that the shearing strain is caused due to the application of tangential force. It is defined as the ratio of relative displacement of the faces $\Delta x$ to the height of the block h. If $\theta$ is the angular displacement of the cylinder from the vertical, then,
Shearing strain =$\tan \theta =\dfrac{\Delta x}{h}$
If $\theta$ is very small,
Shearing strain = $\theta =\dfrac{\Delta x}{h}$
Substituting the given values we get,
$\theta =\dfrac{0.015\times {{10}^{-3}}m}{{{10}^{-2}}m}$
$\therefore \theta =0.0015$
We know that rigidity modulus is given by the ratio of shearing stress to that of shearing strain. Shearing stress, just like any other stress, is the force exerted on unit area. So,
$\eta =\dfrac{\dfrac{F}{A}}{\theta }$
$\Rightarrow F=\eta A\theta$
Substituting the values we get,
$F=4.5\times {{10}^{10}}\times 0.25\times 0.0015$
$\therefore F=16.875\times {{10}^{6}}N$
Therefore, we find the shearing strain of the block to be 0.0015 and the shearing force is found to be$16.875\times {{10}^{6}}N$

Note: Applying shear force could be best explained by the example of deck of cards. When we apply shear force on a deck of cards, they are being pushed one way on the top and other way at the bottom and which further results in sliding of cards. Also while calculating, make sure that you convert the given values into their SI units before substitution.