Question

The area of the smaller of the two circles that touch the parabola ${{y}^{2}}=4x$ at the point $\left( 1,2 \right)$ and the x axis is
A. $4\pi \left( 2-\sqrt{2} \right)$
B. $8\pi \left( 3-2\sqrt{2} \right)$
C. $4\pi \left( 3+\sqrt{2} \right)$
D. $8\pi \left( 2-\sqrt{2} \right)$

Answer 1

To solve this question, we should know the concepts related to conic sections. The slope of tangent at A$\left( 1,2 \right)$ to the curve ${{y}^{2}}=4x$ is given by ${{\left. m=\dfrac{dy}{dx} \right|}_{\left( 1,2 \right)}}$. Using this, we can find the tangent and normal to the parabola at the point A. As the circle and parabola are touching, the tangent and normal are the same for both the curves at the point A. The distance between the centre of the circle and the tangent is equal to the radius of the circle. It is given that the circle is touching the x axis which implies that x-axis is a tangent to the circle. The distance between a point $\left( {{x}_{1}},{{y}_{1}} \right)$ and the line $ax+by+c=0$ is $\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$. The normal passes through the centre of the circle. The three unknowns in the question are centre $C\left( {{x}_{1}},{{y}_{1}} \right)$ and radius r units. We have three relations and we can get the three unknowns. The area of the circle with r units is $A=\pi {{r}^{2}}$

Complete step-by-step answer :

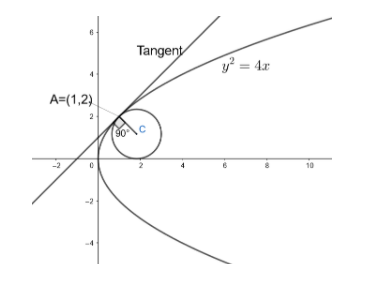
Let us consider the centre of the required circle as $C\left( {{x}_{1}},{{y}_{1}} \right)$ and the radius be r units. We know from the question that the circle touches x-axis and x-axis is a tangent to the circle.
We know that the distance between the centre and tangent of the circle is equal to radius.
The distance between a point $\left( {{x}_{1}},{{y}_{1}} \right)$ and the line $ax+by+c=0$ is $\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$.
Here the equation of the line is $y=0$ and point is $C\left( {{x}_{1}},{{y}_{1}} \right)$ and distance is equal to r units.
$\begin{aligned} & \text{distance}=r=\dfrac{\left| {{y}_{1}} \right|}{\sqrt{{{1}^{2}}}}=\left| {{y}_{1}} \right| \\\ & \left| {{y}_{1}} \right|=r \\\ \end{aligned}$
As the centre is in the first quadrant ${{y}_{1}}=r$. So, the centre is $C\left( {{x}_{1}},r \right)$
Let us consider the parabola ${{y}^{2}}=4x$ and point A$\left( 1,2 \right)$.
The slope of tangent at A$\left( 1,2 \right)$ to the curve ${{y}^{2}}=4x$ is given by ${{\left. m=\dfrac{dy}{dx} \right|}_{\left( 1,2 \right)}}$.
Differentiating ${{y}^{2}}=4x$ with respect to x, we get
$\begin{aligned} & 2y\dfrac{dy}{dx}=4 \\\ & \dfrac{dy}{dx}=\dfrac{4}{2y} \\\ \end{aligned}$
The slope of tangent at $\left( 1,2 \right)$ is given by
${{\left. m=\dfrac{dy}{dx} \right|}_{\left( 1,2 \right)}}=\dfrac{4}{2\times 2}=1$
The product of slopes of two perpendicular lines = -1
As tangent and normal are perpendicular to each other, the slope of normal is given by
$\begin{aligned} & 1\times {{m}_{normal}}=-1 \\\ & {{m}_{normal}}=-1 \\\ \end{aligned}$
Equation of a line passing through point $\left( {{x}_{1}},{{y}_{1}} \right)$ and slope m is given by
$y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
Using this, we can write the equation of the tangent as
$\begin{aligned} & y-2=1\times \left( x-1 \right) \\\ & x-y+1=0 \\\ \end{aligned}$
We can write the equation of the normal as
$\begin{aligned} & y-2=-1\left( x-1 \right) \\\ & x+y-3=0 \\\ & x+y=3 \\\ \end{aligned}$
We know that the tangent and normal at $\left( 1,2 \right)$are the same for the parabola and the circle as both the curves are touching each other at $\left( 1,2 \right)$.
We know that the normal of the circle passes through the centre of the circle. Substituting the centre in the normal, we get
$\begin{aligned} & {{x}_{1}}+r=3 \\\ & {{x}_{1}}=3-r \\\ \end{aligned}$
The centre becomes, $\left( 3-r,r \right)$
We know that the distance between the centre and tangent is equal to radius.
Using this on the centre and the tangent $x-y+1=0$, we get
$\begin{aligned} & \text{distance}=\dfrac{\left| 3-r-r+1 \right|}{\sqrt{{{1}^{2}}+{{1}^{2}}}}=r \\\ & \left| 4-2r \right|=\sqrt{2}r \\\ \end{aligned}$
If we take $4-2r>0$, we get the radius of the smaller circle.
So
$\begin{aligned} & 4-2r=\sqrt{2}r \\\ & r\left( 2+\sqrt{2} \right)=4 \\\ & r=\dfrac{4}{2+\sqrt{2}} \\\ \end{aligned}$
By rationalising, we get
$r=\dfrac{4}{2+\sqrt{2}}\dfrac{2-\sqrt{2}}{2-\sqrt{2}}=\dfrac{4\left( 2-\sqrt{2} \right)}{{{2}^{2}}-{{\left( \sqrt{2} \right)}^{2}}}=\dfrac{4\left( 2-\sqrt{2} \right)}{2}=4-2\sqrt{2}$
So, radius of the smaller circle is $r=4-2\sqrt{2}$
Area of the circle with radius r units is given by $A=\pi {{r}^{2}}$ sq units.
$Area=\pi {{\left( 4-2\sqrt{2} \right)}^{2}}=\pi \left( {{4}^{2}}+{{\left( 2\sqrt{2} \right)}^{2}}-2\times 4\times 2\sqrt{2} \right)=\pi \left( 16+8-16\sqrt{2} \right)$
$Area=\pi \left( 24-16\sqrt{2} \right)=8\pi \left( 3-2\sqrt{2} \right)$
$\therefore Area=8\pi \left( 3-2\sqrt{2} \right)$. The answer is option-B

Note : An alternate way to do this problem is by applying the property that the distance between any point and the centre is equal to radius. Applying this with C$\left( 3-r,r \right)$ and A$\left( 1,2 \right)$, we get
$\begin{aligned} & \sqrt{{{\left( 3-r-1 \right)}^{2}}+{{\left( r-2 \right)}^{2}}}=r \\\ & 2\times {{\left( r-2 \right)}^{2}}={{r}^{2}} \\\ & 2{{r}^{2}}-8r+8={{r}^{2}} \\\ & {{r}^{2}}-8r+8=0 \\\ & r=\dfrac{8\pm \sqrt{{{8}^{2}}-4\times 8}}{2}=4\pm 2\sqrt{2} \\\ \end{aligned}$
The smaller radius is $r=4-2\sqrt{2}$.