Question

The area of the region \left\\{ \left( x,y \right):xy\le 8,1\le y\le {{x}^{2}} \right\\} is:
(a)$16{{\log }_{e}}2-6$
(b)$8{{\log }_{e}}2-\dfrac{7}{3}$
(c) $16{{\log }_{e}}2-\dfrac{14}{3}$
(d) $8{{\log }_{e}}2-\dfrac{14}{3}$

Answer 1

First of all draw the inequalities given in the above question on the graph paper and then find the intersected area and mark that area. After that using a method of integration, find the area of the intersected region of the inequalities. We know that, area under the curve using the method of integration is found by using the following formula $\int\limits_{a}^{b}{ydx}$. In this formula, substitute y in terms of x so that we are able to evaluate the integral.

Complete step-by-step answer :
We have given the following inequalities as:
\left\\{ \left( x,y \right):xy\le 8,1\le y\le {{x}^{2}} \right\\}
And we have to find the common area which is intersected by the three inequalities.
In the below figure, we have drawn the three inequalities on the graph we get,

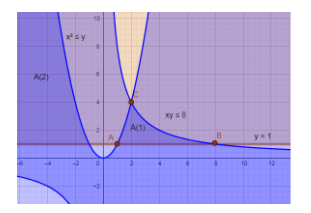
In the above figure, the common region which is intersected by the three inequalities is A(1) and A(2) but A(2) is the unbounded area so we are only finding the area of bounded region i.e. A(2).
Now, we are going to find the coordinates of A, B and C.
Point A is the intersection of the parabola ${{x}^{2}}=y$ and the line $y=1$ so substituting the value of y as 1 in the equation of a parabola we get the x coordinates of point A.
$\begin{aligned} & {{x}^{2}}=1 \\\ & \Rightarrow x=\pm 1 \\\ \end{aligned}$
As point A lies on the positive x axis so we are rejecting the negative value of x so the x coordinates of point A is:
$x=1$
Hence, we have got the coordinates of point A (1, 1).
Now, the y coordinates of point B we know that is 1 so x coordinates is calculated by substituting the value of y as 1 in $xy=8$ we get,
$\begin{aligned} & x\left( 1 \right)=8 \\\ & \Rightarrow x=8 \\\ \end{aligned}$
Hence, we got the coordinates of point B as (8, 1).
Now, to find the coordinates of point C we have to find the intersection of ${{x}^{2}}=y\And xy=8$ which we are going to do as follows:
$\begin{aligned} & xy=8 \\\ & \Rightarrow y=\dfrac{8}{x} \\\ \end{aligned}$
Substituting the value of y in ${{x}^{2}}=y$ we get,
$\begin{aligned} & {{x}^{2}}=\dfrac{8}{x} \\\ & \Rightarrow {{x}^{3}}=8 \\\ \end{aligned}$
Taking cube root on both the sides we get,
$x=2$
Substituting the above value of x in $y=\dfrac{8}{x}$ we get,
$\begin{aligned} & y=\dfrac{8}{2} \\\ & \Rightarrow y=4 \\\ \end{aligned}$
Hence, we got the coordinates of point C as (2, 4).
Now, to find the area of region A (1) we have to find the area from A to C then the area from C to B.

The area under the curve is calculated by using the method of integration in which we integrate the area under the curve within some limits.
$\int\limits_{a}^{b}{ydx}$
This is how, area under the curve is calculated.
Now, we are going to find the area from A to C we get,
$\int\limits_{1}^{2}{\left( {{x}^{2}}-1 \right)dx}$
As you can see from the figure that x coordinates from A to C is 1 to 2 and the bounded region is made by the parabola ${{x}^{2}}=y$ and the straight line $y=1$. That’s why we put y as the difference of the parabola and the straight line.

& \int\limits_{1}^{2}{{{x}^{2}}}dx-\int\limits_{1}^{2}{dx} \\\ & =\left| \dfrac{{{x}^{3}}}{3} \right|_{1}^{2}-\left| x \right|_{1}^{2} \\\ \end{aligned}$$ Applying the lower and upper limit we get, $\begin{aligned} & \dfrac{1}{3}\left[ {{\left( 2 \right)}^{3}}-1 \right]-\left( 2-1 \right) \\\ & =\dfrac{1}{3}\left[ 8-1 \right]-1 \\\ & =\dfrac{7}{3}-1 \\\ & =\dfrac{4}{3} \\\ \end{aligned}$ Hence, we got the area of the bounded region from A to C is $\dfrac{4}{3}$. Now, we are going to find the area bounded by hyperbola $xy=8$ and $y=1$ from C to B by subtracting the y of the straight line from the hyperbola and the limits of x are from 2 to 8. $\begin{aligned} & \int\limits_{2}^{8}{\left( \dfrac{8}{x}-1 \right)}dx \\\ & =\int\limits_{2}^{8}{\dfrac{8}{x}}dx-\int\limits_{2}^{8}{dx} \\\ & =8\left| {{\log }_{e}}x \right|_{2}^{8}-\left| x \right|_{2}^{8} \\\ \end{aligned}$ Applying the lower and upper limits we get, $8\left( {{\log }_{e}}8-{{\log }_{e}}2 \right)-\left( 8-2 \right)$ There is a property of logarithm that: ${{\log }_{e}}a-{{\log }_{e}}b={{\log }_{e}}\dfrac{a}{b}$ Using this property in the above we get, $8\left( {{\log }_{e}}\dfrac{8}{2} \right)-6$ $=8{{\log }_{e}}4-6$ Hence, we got the area bounded the curves from C to B is equal to $8{{\log }_{e}}4-6$. Now, adding the areas of the bounded region from A to C and C to B we get, $\begin{aligned} & \dfrac{4}{3}+8{{\log }_{e}}4-6 \\\ & =\dfrac{4-18}{3}+8{{\log }_{e}}4 \\\ & =-\dfrac{14}{3}+8{{\log }_{e}}4 \\\ \end{aligned}$ Hence, we got the area bounded by the inequalities as $-\dfrac{14}{3}+8{{\log }_{e}}4$. Now, on comparing the above area with the options, we found that options containing the term ${{\log }_{e}}2$ so we have to convert our area into this term. Converting our area that we got into this term we get, $-\dfrac{14}{3}+8{{\log }_{e}}{{\left( 2 \right)}^{2}}$ Using the following property in the above expression we get, ${{\log }_{e}}{{a}^{b}}=b{{\log }_{e}}a$ $\begin{aligned} & -\dfrac{14}{3}+8\left( 2 \right){{\log }_{e}}\left( 2 \right) \\\ & =-\dfrac{14}{3}+16{{\log }_{e}}\left( 2 \right) \\\ \end{aligned}$ Hence, the correct option is (c). **Note** : You might think that we have got the two common areas A(1) and A(2) then why we only calculate the bounded area i.e. A(1) because the unbounded area A(2) will give us the indefinite answer because the region is unbounded so there is an uncertainty or non definitiveness so we haven’t calculated the area of the unbounded region and only show the area of the bounded region.