Question

The area of the region enclosed by the curves $y = x,x = e,y = 1/x$ and positive x-axis is
A.$3/2$ square units
B.$5/2$ square units
C.$1/2$ square units
D.1 square units

Answer 1

Here we will first draw all the given curves and find the bounded area. Then we will use the integration method to find the area of the bounded area or required area. Then by solving it we will get the area bounded by the given curves.

Complete step-by-step answer:
The curves given are $y = x,x = e,y = 1/x$.
Firstly we will draw the curves on the Cartesian plane to get the bounded region. Therefore, we get

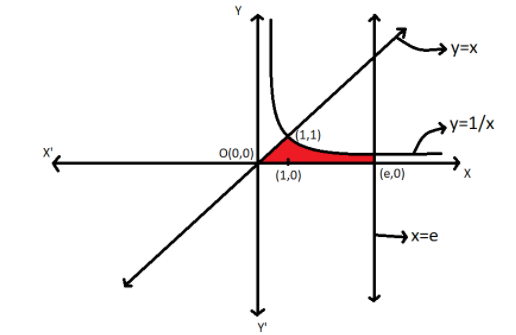
We can see that the red shaded region is the required region and we have to calculate the area of this region. By using the basic concept of the integration we will find the area of the shaded region. Therefore, we get
Area of the shaded region $= \int\limits_0^1 {xdx} + \int\limits_1^e {\dfrac{1}{x}dx}$
Now we will solve this equation by using the integration to get the required area. Therefore, we get
$\Rightarrow$ Area of the shaded region $= \left( {\dfrac{{{x^2}}}{2}} \right)_0^1 + \left( {\log \left( x \right)} \right)_1^e$
Now by putting the limits in the brackets, we get
$\Rightarrow$ Area of the shaded region $= \left( {\dfrac{1}{2} - 0} \right) + \left( {\log \left( e \right) - \log 1} \right)$
$\Rightarrow$ Area of the shaded region $= \left( {\dfrac{1}{2}} \right) + \left( {1 - 0} \right) = \dfrac{3}{2}$ square units
Hence, the area of the region enclosed by the curves $y = x,x = e,y = 1/x$ and positive $x$-axis is $3/2$ square units.
So, option A is the correct option.

Note: We should write the proper coordinates of the intersection of the curves on the Cartesian plane as it is used to get the limits of the integration part of the equation to find out the area of the bounded region. While writing the coordinates of a point always the X-axis intercept of the point is written first and then the Y-axis intercept is written. Also in the representation of this axis in the Cartesian plane are perpendicular to each other and intersecting at a point which is named as the origin. We should remember that the positive X-axis is towards the right side of the origin and the negative X-axis is towards the left side of the origin. Also the positive Y-axis is towards the upward direction from the origin and negative Y-axis is towards the downward direction from the origin.